1. Einleitung
Einen Abstand zwischen einer Geraden und einer Ebene zu bestimmen ist grundsätzlich nicht sehr schwer. Wie bei der Abstandsberechnung zwischen zwei Ebenen gibt es auch hier drei verschiedene Varianten, wie Ebene und Gerade zueinander liege. Je nach ihrer Lage zueinander kann man beurteilen, ob man überhaupt rechnen muss oder nicht.
- Gerade liegt in der Ebene:
Hier ist der Abstand logischerweise null. - Gerade und Ebene schneiden:
Auch hier ist der Abstand null, da nur der geringste Abstand zwischen Gerade und Ebene zählt. Dieser geringste Abstand liegt am Schnittpunkt, wo er null ist. - Gerade und Ebene sind parallel:
Der einzige Fall, den man wirklich untersuchen muss. Das Vorgehen ist mehr oder weniger gleich mit dem bei der Messung des Abstandes zwischen zwei Ebenen. Zuerst bildet man die Hessesche Normalenform der Ebene. Danach sucht man sich einen Punkt auf der Geraden. Den Punkt setzt man in die Hessesche Normalenform ein. Das Ergebnis ist der Abstand - fertig.
2. Gerade liegt in Ebene
Auf dem Bild kann man gut sehen, dass die Gerade (rot) keinen Abstand zur Ebene (grün) hat (bzw. dass der Abstand null beträgt).
Wenn man prüfen will, ob eine Gerade in einer Ebene liegt, muss man nach der gegebenen Ebenenform vorgehen:
- Die Ebene ist in Koordinatenform oder in Normalenform gegeben:
Zuerst prüft man, ob der Richtungsvektor orthogonal zum Normalenvektor der Ebene liegt (= ist das Skalarprodukt der beiden Vektoren gleich null? Wenn ja, dann liegen sie im rechten Winkel zueinander, also orthogonal). Liegen sie orthogonal zueinander, dann schaut man, ob ein Punkt der Geraden in der Ebene liegt, oder umgekehrt. Liegt ein Punkt der Geraden in der Ebene, dann liegt auch die ganze Gerade in der Ebene. - Die Ebene ist in Parameterform gegeben:
Hier muss man zuerst den Normalenvektor errechnen, z.B. indem man das Vektorprodukt aus den beiden Richtungsvektoren der Geraden bildet. Danach geht man genauso weiter vor wie bei der Koordinatenform/Normalenform.
3. Gerade und Ebene schneiden
Auch wenn eine Gerade eine Ebene schneidet ist der Abstand logischerweise null, denn so "groß" ist der Abstand an der Stelle an der Gerade und Ebene am nächsten zueinander liegen: Am Schnittpunkt.
Um herauszufinden, ob sich Gerade und Ebene schneiden, kann man einfach die oben aufgeführte Vorgehensweise erweitern. Ist nämlich der Richtungsvektor der Geraden nicht orthogonal zur Ebene, dann müssen sich Ebene und Gerade früher oder später schneiden. Die Gerade liegt dann im Vergleich zur Ebene grob gesagt "schief", wie auch im Bild zu sehen ist. Da Ebenen und Geraden unendlich weit laufen, werden sie sich in diesem Fall immer schneiden - und somit den Abstand 0 haben.
4. Gerade und Ebene liegen parallel
Der einzige Fall bei dem man richtig rechnen muss. Die Rechnung ist aber zum Glück nicht sehr schwer.
Wie beim Abstand zwischen Ebene und Ebene gibt es auch beim Abstand zwischen Ebene und Gerade keine einzelnen zwei Punkten, die den geringsten Abstand zueinander haben. Stattdessen gibt es für jeden Punkt auf der Geraden auch einen Punkt auf der Ebene, der gleich mit dem allgemeinen Abstand zwischen Gerade und Ebene ist:
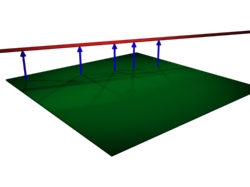
Gerade (rot) und Ebene (grün) liegen parallel zueinander.
Die blauen Pfeile zeigen, dass der Abstand zwischen Gerade und Ebene überall gleich ist.
Das Vorgehen ist hier zunächst wieder ähnlich wie unter Punkt 1 (Gerade liegt in Ebene), da man auch hier erstmal schauen muss, ob Gerade und Ebene überhaupt parallel sind. Grundsätzlich laufen dazu alle Schritte gleich ab wie unter Punkt 1, aber mit einem Unterschied: Wenn man prüft, ob ein Punkt der Geraden in der Ebene liegt, dann muss man ein unwahres Ergebnis erhalten. Das heißt, dass ein Punkt der Geraden nicht in der Ebene liegen darf. Denn laufen Ebene und Gerade in ähnliche Richtungen (also nicht "schief" wie wenn sie sich schneiden), dann gibt es nur die beiden Möglichkeiten, dass entweder alle Punkte von der Geraden in der Ebene sind (Gerade liegt in Ebene), oder dass kein Punkt der Geraden in der Ebene liegt (Gerade ist parallel zur Ebene).
Also: Alles wie bei Punkt eins, nur wenn man testet ob ein Punkt der Geraden in der Ebene liegt, dann muss man ein unwahres Ergebnis erhalten.
Beispiel:
Gegeben sind eine Ebene und eine Gerade.
Aus der Ebene kann man schnell den Normalenvektor (n) herausfiltern:
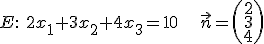
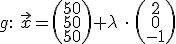
1. Prüfen, ob Ebene und Gerade parallel sind
1.1. Ist der Richtungsvektor der Geraden orthogonal zum Normalenvektor?
Überprüft wird das mit Hilfe des Skalarprodukts:
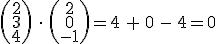
1.2. Liegt ein Punkt der Geraden in der Ebene?
Überprüft wird das indem man einen Punkt der Geraden einsetzt
(Stützvektor der Geraden wird eingesetzt, da der auf der Geraden liegen muss):
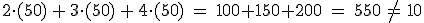
Da der Punkt nicht in der Ebene lag müssen Ebene und Gerade parallel sein.
Man kann also mit der Berechnung des Abstandes fortfahren.
2. Abstandsberechnung
2.1. Hessesche Normalenform (HNF) bilden:
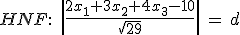
2.2. Punkt auf der Geraden wird in die HNF eingesetzt (hier: Ihr Stützvektor)
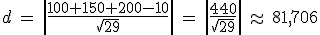
Fertig: Der Abstand ist etwa 81,706 Längeneinheiten.
Aus der Ebene kann man schnell den Normalenvektor (n) herausfiltern:
1. Prüfen, ob Ebene und Gerade parallel sind
1.1. Ist der Richtungsvektor der Geraden orthogonal zum Normalenvektor?
Überprüft wird das mit Hilfe des Skalarprodukts:
1.2. Liegt ein Punkt der Geraden in der Ebene?
Überprüft wird das indem man einen Punkt der Geraden einsetzt
(Stützvektor der Geraden wird eingesetzt, da der auf der Geraden liegen muss):
Da der Punkt nicht in der Ebene lag müssen Ebene und Gerade parallel sein.
Man kann also mit der Berechnung des Abstandes fortfahren.
2. Abstandsberechnung
2.1. Hessesche Normalenform (HNF) bilden:
2.2. Punkt auf der Geraden wird in die HNF eingesetzt (hier: Ihr Stützvektor)
Fertig: Der Abstand ist etwa 81,706 Längeneinheiten.
5. Anmerkungen
- Wenn schon durch die Aufgabe vorgegeben ist, dass Ebene und Gerade parallel liegen, dann kann man sich das Überprüfen natürlich sparen und direkt den Abstand errechnen. Das spart einige Zeit ein.

