Druckversion: Parameterform (Vektorrechnung)

1. Einleitung

Die Parameterform ist am ehesten vergleichbar mit der Darstellung von Geraden.
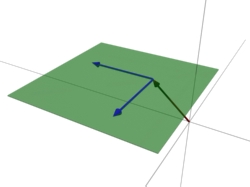
Eine typische Gerade:

Bei dieser Darstellung zeigt der Stützvektor auf einen bestimmten Punkt im Raum, hier auf

. Von dort aus geht der Richtungsvektor ab. Dieser kann durch die Variable

(lambda) beliebig in seiner Länge verändert werden. Dadurch kann jeder Punkt auf der Geraden bestimmt werden. Man hat also in gewisser Weise ein Koordinatensystem im Raum, bei dem der Stützvektor auf den Ursprung zeigt und von dem der Richtungsvektor abgeht - als einzige Achse des Koordinatensystems.

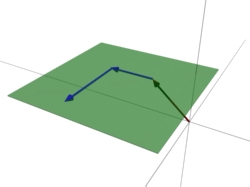
Das einzige was sich bei der Ebenendarstellung ändert ist, dass sozusagen eine zweite Achse dazukommt. Ist ja auch logisch, denn eine Ebene ist ja eine Fläche, nicht eine Gerade und um eine Fläche zu bestimmen, braucht man nunmal zwei Achsen. Zeichnet man ein zweidimensionales Koordinatensystem auf ein Blatt Papier, dann kann man jeden Punkt auf diesem Blatt bestimmen - man muss nur die entsprechenden x und y-Werte haben.

Bild 1: Eine Ebene in Parameterform. Die beiden Richtungsvektoren sind blau, der Stützvektor ist rot (verdeckt von Ebene). Die Ebene selbst ist grün und leicht durchsichtig.

Bild 2: Beispiel wie man zu einem Punkt in der Ebene kommt. Erst den Stützvektor folgen, dann

mal der erste Richtungsvektor, dann

mal der zweite Richtungsvektor.

Bild 3: Je nachdem wie man die Variablen für die Richtungsvektoren setzt kann man auf jeden Punkt in der Ebene zeigen. Man kann natürlich auch Minuszahlen einsetzen, sodass die Vektoren in die entgegengesetzte Richtung zeigen.

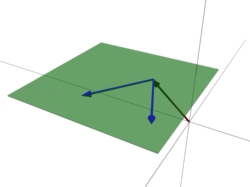
Bild 4: Eine zweite Beispielebene in Parameterform: Die Richtungsvektoren müssen nicht zwangsweise im 90°-Winkel liegen! Sie dürfen nur nicht linear abhängig voneinander sein. Denn dann würden sie in die selbe Richtung zeigen (oder in die genau entgegengesetzte) und keine Ebene, sondern eine Gerade bilden! (siehe auch Anmerkungen)

2. Darstellung

Um eine zweite "Achse" zu haben brauchen wir erstmal eine zweite Variable. Dafür nehmen wir

(ausgesprochen: "Müh"). Außerdem wird ein zweiter Richtungsvektor benötigt.

allgemeine Darstellungsform:

$E: x=(s_1,s_2,s_3)+lambda*(r_{11},r_{12},r_{13})+mu*(r_{21},r_{22},r_{23})$

Hierbei ist

der Ortsvektor zu jeden beliebigen Punkt in der Ebene. Gewöhnlich wird dieser Vektor nur

geschrieben, man kann aber auch

schreiben. Dieser Vektor wird gewöhnlich variabel gehalten (das heißt, dass man die x stehen lässt). Damit zeigt man, dass jeder Punkt, der durch den Teil der Gleichung hinter dem Gleichzeichen definiert wird, in dieser Ebene liegt. Nur dann wenn man überprüft, ob ein Punkt in der Ebene liegt, dann setzt man für

den Vektor zu diesem Punkt ein. (Dann ergibt sich ein lineares Gleichungssystem, das rechnet man aus und wenn man für die Variablen reelle Zahlen als Ergebnis erhält, dann liegt der Punkt in der Ebene).

Soviel zu

ist hier wieder der Stützvektor, der sozusagen den Ursprung festlegt.

und

sind die beiden Richtungsvektoren, deren Länge verändert wird, um so jeden Punkt in der Ebene darstellen zu können.

Beispiel:

Hier kann man dann z.B. sehen, dass das x variabel gehalten ist. Es ist jeder Punkt in der Ebene gemeint, der sich durch die nachstehenden Vektoren und durch das einsetzen von Zahlen in die Variablen bilden lässt. Diese unendlich große Menge an Punkten ergibt eine Ebene!

3. Anmerkungen

Der erste und der zweite Richtungsvektor dürfen nicht linear abhängig sein, sonst hat man nur eine Geradengleichung mit zwei Variablen - und kann wieder nur Punkte auf der Geraden darstellen. Es ist so, als wollte man ein zweidimensionales Koordinatensystem aufbauen, indem man zwei mal die x-Achse verwendet. Da kann man natürlich auf keinen Punkt zeigen, der einen y-Wert ungleich 0 hat.

4. Links

Und noch ein kleines Video, das das Bilden der Parameterform verdeutlicht.

Parameterform (Thema: Vektorrechnung)

Ebenen darstellen mit Hilfe der Parameterform