Druckversion: Gesetz der großen Zahl (Stochastik)

Schnellübersicht

Je häufiger ein Zufallsexperiment wiederholt wird, desto mehr nähert sich die gemessene relative Häufigkeit der tatsächlichen Wahrscheinlichkeit an.
Jede einzelne Wiederholung bleibt aber trotzdem unabhängig von allen anderen Wiederholungen. (Wurde 9 mal Wappen geworfen, dann folgt noch immer mit 50%-iger Wahrscheinlichkeit ein zehntes mal Wappen.)

1. Einleitung

Es wurde zuvor gezeigt, dass sich anhand der relativen Häufigkeit die Wahrscheinlichkeit eines Ereignisses in Bezug auf eine Menge von Messdaten bestimmen lässt. Diese gemessene Wahrscheinlichkeit ist aber nicht konstant, sondern hängt von der Anzahl der Wiederholungen und den Ergebnissen der einzelnen Wiederholungen ab. Die auf diesem Weg bestimmte Wahrscheinlichkeit kann zum Teil deutlich von der tatsächlichen Wahrscheinlichkeit abweichen.
Beispiel: Angenommen wir werfen eine Münze. Nach der Laplace-Formel haben die Ereignisse Wappen und Zahl beide eine Eintrittswahrscheinlichkeit von 0,5. Werfen wir nun zwei mal die Münze und erhalten beide male Wappen, dann liegt die Wahrscheinlichkeit für das Ereignis EWappen nach der relativen Häufigkeit bei 1 bzw. 100%. Werfen wir nun die Münze 10 weitere male und erhalten 8 mal Wappen und 2 mal Zahl, dann liegt nach der relativen Häufigkeit die Wahrscheinlichkeit für EWappen bei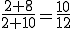 $Formel-Code: \frac{2+8}{2+10}=\frac{10}{12}$ , was ungefähr 0,83 entspricht. Der Wert ist demnach gesunken, aber noch immer zu hoch. Werfen wir die Münze noch öfter, dann sollte sich der Wert langsam dem erwarteten Wert von 0,5 annähern.

Ein beispielhafter Verlauf für den Münzwurf könnte wie folgt aussehen:

	5. Wurf	25. Wurf	100. Wurf	500. Wurf
Anteil Wappen	0,8	0,72	0,57	0,51

Mit zunehmender Zahl an Wiederholungen nähert sich der gemessene Wert für die relative Häufigkeit der tatsächlichen Wahrscheinlichkeit an.

2. Wieso ist das so?

Nun mag es intuitiv offensichtlich sein, dass sich (zum Beispiel) bei einem Münzwurf die Wahrscheinlichkeit mit zunehmender Anzahl an Würfen dem Wert 0,5 annähert. Das erklärt allerdings nicht mathematisch wieso das der Fall ist.
Die genauere Erklärung lässt sich schlicht umschreiben mit: es wird immer unwahrscheinlicher mit der Münze eine Kombination zu werfen, die weit abseits von 0,5 liegt. Diese meisten der möglichen Kombinationen liegen nämlich nahe bei 0,5 und jede einzelne Kombination hat die selbe Wahrscheinlichkeit geworfen zu werden (nach Laplace-Formel). Angenommen wir kürzen Wappen mit W und Zahl mit Z ab und schreiben Kombinationen in der Form {W, W, Z} für Wappen (1. Wurf), Wappen (2. Wurf) und Zahl (3. Wurf).
Für zwei Münzwürfe erhalten wir dann folgende Tabelle:

Anzahl Wappen	Kombinationen	Anzahl Kombinationen
0	{K, K}	1
1	{W, K}, {K, W}	2
2	{W, W}	1

Bei zwei Münzwürfen gibt es demnach 2 Kombinationen, bei denen eine Seite in mindestens 75% der Fälle geworfen wird und 2 Kombinationen, die genau bei <75% Anteil für beide Seiten liegen. Demnach liegt die Wahrscheinlichkeit, eine Kombination zu treffen, die nicht 0,5 entspricht bei 2/4, also 0,5 bzw. 50%.

Für drei Münzwürfe:

Anzahl Wappen	Kombinationen	Anzahl Kombinationen
0	{K, K, K}	1
1	{W, K, K}, {K, W, K}, {K, K, W}	3
2	{W, W, K}, {W, K, W}, {K, W, W}	3
3	{W, W, W}	1

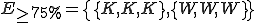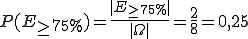Wie der Tabelle zu entnehmen ist gibt es bei drei Münzwürfen schon nur noch zwei Fälle in denen eine der Seiten in mindestens 75% aller Fälle geworfen wird, gegenüber 6 bei denen beide Seiten eine Wahrscheinlichkeit unter 75% haben. Mathematisch ausgedrückt gilt für $Formel-Code: E_{\geq 75%}=\{\{K,K,K\},\{W,W,W\}\}$ und $Formel-Code: P(E_{\geq 75%}) = \frac{|E_{\geq 75%}|}{|\Omega|}=\frac{2}{8}=0,25$ . 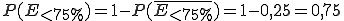Entsprechend gilt für E<75%: $Formel-Code: P(E_{<75%})=1-P(\overline{E_{<75%}})=1-0,25=0,75$ .

Wichtig: Jeder einzelne Münzwurf bleibt unabhängig von den anderen. Wenn man also 9 mal hintereinander Wappen geworfen hat, dann ist die Wahrscheinlichkeit für den nächsten Wurf ebenfalls Wappen zu erhalten noch immer 0,5 bzw. 50%.

2.1. Experiment

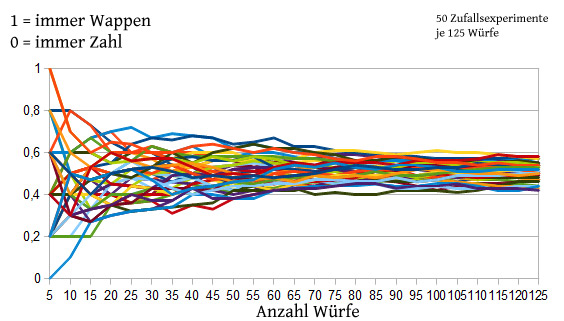
Das weiter unten dargestellte Bild zeigt 50 Zufallsexperimente mit Münzwürfen. Jedes der Experimente beinhaltete 125 Münzwürfe. Gezählt wurde die relative Häufigkeit einer Münzseite. Wie zu sehen ist, gibt es am Anfang eine große Schwankungsbreite, die gegen Ende hin immer geringer wird.

50 Zufallsexperimente, je 125 Münzwürfe. Werte nahe 0,5 heißen, dass beide Münzseiten gleich häufig geworfen wurden.

3. Formel für das Gesetz der großen Zahl

Die Formel für das Gesetz der großen Zahl lautet

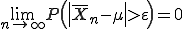$Formel-Code: \lim_{n\to\infty}P\left(\left|\overline{X}_n-\mu\right|>\varepsilon\right) = 0$

mit n der Anzahl an Wiederholungen des Zufallsexperiments, 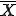$Formel-Code: \overline{X}$ dem Mittelwert aller Ergebnisse, μ dem erwarteten Mittelwert und ε einer beliebig kleinen positiven Zahl.
Angenommen beim Münzwurf wird Wappen eine 1 und Zahl eine 0 zugewiesen, dann ergäbe sich der Mittelwert der Kombination {W, K, W, W} zum Beispiel aus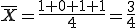 $Formel-Code: \overline{X}=\frac{1+0+1+1}{4}=\frac{3}{4}$ . Der erwartete Mittelwert (Erwartungswert) μ wiederum lautet für den Münzwurf 0,5.
In Abschnitte unterteilt besagt die Formel:

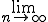$Formel-Code: \lim_{n\to\infty}$ : Nach nahezu unendlich vielen Wiederholungen des Zufallsexperiments...

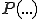: ...ist die Wahrscheinlichkeit...

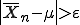$Formel-Code: \left|\overline{X}_n-\mu\right|>\varepsilon$ : ...dass der ermittelte Mittelwert vom Erwartungswert abweicht (egal wie wenig und egal ob positiv (>0) oder negativ (<0))..

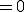: ...gleich null.

Hinweis: Die hier beschriebene Formel gilt für das sogenannte schwache Gesetz der großen Zahl. Es gibt auch ein starkes Gesetz, jedoch sollte das schwache Gesetz zum Verständnis des Themas reichen.

4. Quiz

Nach wie vielen der unten aufgeführten Münzwürfe ist am ehesten damit zu rechnen, dass der Anteil von Wappen zwischen 45% und 55% liegt?

Nach 12

Nach 194.482

Nach 10.000

Die Anzahl der Würfe spielt keine Rolle

#6965

Angenommen man wirft einen Würfel eine Million mal. Welche relative Häufigkeit kann man am Ende für die Augenzahl 6 ungefähr erwarten?

Etwa 1/6

Etwa 6

Etwa 1/2

Etwa 1

#6966

Herr Donald Duck besucht ein Casino und stellt sich an einen Roulettetisch. Da er viel von Stochastik versteht, beobachtet er das Spiel und wartet geduldig auf seine Chance. Nach einigen Stunden ist sie schließlich da: schon sechs mal landete die Kugel nacheinander auf der Zahl 11! Wie hat dies die Wahrscheinlichkeit beeinflusst, dass die Kugel nun direkt noch mal auf der 11 landet?

Die Wahrscheinlichkeit ist gesunken

Die Wahrscheinlichkeit ist gleich geblieben

Die Wahrscheinlichkeit ist gestiegen

#6967

5. Links

Relative und absolute Häufigkeit für verschiedene Augenzahlen und Wiederholungen testen: http://www.jakob-wankel.de/temp/zufall.php
Wikipedia zum Gesetz der großen Zahl (englisch)
http://mathworld.wolfram....eakLawofLargeNumbers.htmlBeweis des schwachen Gesetzes der großen Zahl

Gesetz der großen Zahl (Thema: Stochastik)

In diesem Artikel wird das schwache Gesetz der großen Zahl erläutert, wieso es gilt und welche Auswirkungen es auf die gemessene relative Häufigkeit hat.