Schnellübersicht
Zuvor wurde erläutert, dass Ereignisse Mengen von Elementarereignissen sind und welche grundsätzlichen Operationen für Mengen zur Verfügung stehen (speziell Vereinigungsmenge und Schnittmenge). Dementsprechend ist es möglich, Ereignisse mit Hilfe dieser Operationen zu verbinden, sogenannte verknüpfte Ereignisse. Solch eine Berechnung könnte ungefähr wie folgt aussehen: P(A ∪ B) = ... = 0,5. Es folgen einige Beispiele.
Definieren wir für den Würfelwurf die Ereignisse Egerade = {2, 4, 6} und Eungerade = {1, 3, 5}. Es gilt nun:
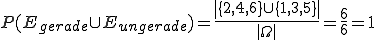
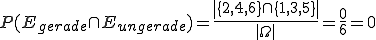
Angenommen wir würfeln mit zwei Würfeln gleichzeitig. Wie hoch ist die Wahrscheinlichkeit, zwei mal die selbe Augenzahl zu erhalten, wenn keiner der Würfel eine 5 sein darf?
Stellen wir zunächst einmal die Ereignisse auf (die Augenzahlen werden hier einfach direkt nebeneinander geschrieben, also z. B. 46 für Augenzahl 4 und Augenzahl 6): Epasch={11, 22, 33, 44, 55, 66}, E5={15, 25, 35, 45, 55, 65, 51, 52, 53, 54, 56}.
nun rechnen wird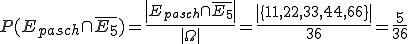
Hinweis: Es gilt |Ω|=36, da es bei zwei Würfeln 6*6=36 mögliche Kombinationen gibt.
In diesem Beispiel sollen einige häufig genutzte Verknüpfungen von Ereignissen eingeführt werden. Wir wählen dazu für den Würfelwurf die Ereignisse A={3, 4}, B={4, 5} und C={6}. Man könnte nun etwa die Wahrscheinlichkeiten folgender verknüpfter Ereignisse ausrechnen:
A oder B:
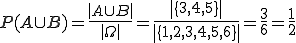
A oder B oder C:
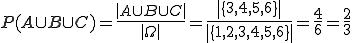
A und B (gleichzeitig):
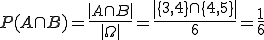
Entweder A oder B (= A oder B, aber nicht A und B gleichzeitig):
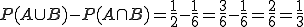
Alternative Rechnung: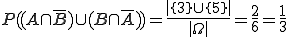
Hinweis: Die etwas kompliziertere Menge aus der alternativen Rechnung heißt soviel wie „jedes Elementarereignis aus A, das nicht in B ist oder jedes Elementarereignis aus B, das nicht in A ist”.
Weder A noch B:
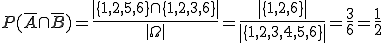
Alternative Rechnung: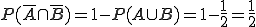

Eine weitere wichtige Regel ist die sogenannte Summenregel. Es gilt:
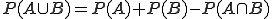 .
.
Übersetzt heißt das: Die Wahrscheinlichkeit von A oder B (P(A ∪ B)) ist identisch (=) mit der Wahrscheinlichkeit von A (P(A)) plus der Wahrscheinlichkeit von B (P(B)) minus der Wahrscheinlichkeit von A und gleichzeitig B (P(A ∩ B)).
Wieso muss P(A ∩ B) abgezogen werden? Das liegt daran, dass A und B gemeinsame Elementarereignisse enthalten können. Ist dies der Fall, dann würden die Wahrscheinlichkeiten dieser Elementarereignisse in P(A) sowie in P(B) berücksichtig und dadurch doppelt gezählt werden. Subtrahiert man aber P(A ∩ B), dann wird dieser Fehler korrigiert indem jede doppelt gezählte Wahrscheinlichkeit einmal abgezogen wird.
Nimmt man etwa beispielhaft an, dass gilt A=Ω und B=Ω, dann würde für P(A ∪ B) gelten P(Ω) + P(Ω) – P(Ω ∩ Ω) = 1 + 1 - 1 = 1. Ohne die Subtraktion von P(A ∩ B) hingegen: P(Ω) + P(Ω) = 2.
Nutzen der Summenformel: Es kann vorkommen, dass eine der beiden Seiten der Gleichung deutlich einfacher zu rechnen ist als die andere. In diesen Fällen spart man sich durch die Anwendung der Summenformel viel Zeit ein.
Ein weiterer Nutzen ist, dass man zur Bestimmung von Wahrscheinlichkeiten nicht mehr zwangsweise die Mengen der Ereignisse kennen muss. Sind stattdessen etwa die Werte von P(A), P(B) und P(A ∩ B) bekannt, dann kann P(A ∪ B) aus diesen abgeleitet werden.
Zwei Ereignisse gelten als unvereinbar, wenn ihre Schnittmenge die leere Menge ist: A ∩ B = ∅ → A und B sind unvereinbar
Wenn zwei Ereignisse unvereinbar sind, dann können sie nie gleichzeitig eintreten, denn beide Ereignisse haben dann kein einziges gemeinsames Elementarereignis.
Beispiel: Definieren wir für den Würfelwurf Agerade={2, 4, 6} und Bungerade={1, 3, 5}, dann gilt für Agerade ∩ Bungerade = ∅. Agerade und Bungerade haben keine gemeinsamen Elementarereignisse und können daher nicht gleichzeitig eintreten. Anders ausgedrückt: Man kann nicht gleichzeitig eine gerade und eine ungerade Augenzahl würfeln.




- Ereignisse sind Mengen von Elementarereignissen. Mehrere Ereignisse können mit Mengenoperationen (Schnittmenge/∩, Vereinigungsmenge/∪) verknüpft werden (=verknüpfte Ereignisse).
- Einfache Regeln:
- Ereignis A oder B: P(A ∪ B)
- A und B: P(A ∩ B)
- Schwierigere Regeln:
- Entweder A oder B:
- Weder A noch B:
- Höchstens eines von beiden:
- Entweder A oder B:
- Summenregel: P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
1. Einleitung
Zuvor wurde erläutert, dass Ereignisse Mengen von Elementarereignissen sind und welche grundsätzlichen Operationen für Mengen zur Verfügung stehen (speziell Vereinigungsmenge und Schnittmenge). Dementsprechend ist es möglich, Ereignisse mit Hilfe dieser Operationen zu verbinden, sogenannte verknüpfte Ereignisse. Solch eine Berechnung könnte ungefähr wie folgt aussehen: P(A ∪ B) = ... = 0,5. Es folgen einige Beispiele.
2. Beispiele für verknüpfte Ereignisse
2.1. Beispiel 1
Definieren wir für den Würfelwurf die Ereignisse Egerade = {2, 4, 6} und Eungerade = {1, 3, 5}. Es gilt nun:
2.2. Beispiel 2
Angenommen wir würfeln mit zwei Würfeln gleichzeitig. Wie hoch ist die Wahrscheinlichkeit, zwei mal die selbe Augenzahl zu erhalten, wenn keiner der Würfel eine 5 sein darf?
Stellen wir zunächst einmal die Ereignisse auf (die Augenzahlen werden hier einfach direkt nebeneinander geschrieben, also z. B. 46 für Augenzahl 4 und Augenzahl 6): Epasch={11, 22, 33, 44, 55, 66}, E5={15, 25, 35, 45, 55, 65, 51, 52, 53, 54, 56}.
nun rechnen wird
Hinweis: Es gilt |Ω|=36, da es bei zwei Würfeln 6*6=36 mögliche Kombinationen gibt.
3. Häufig genutzte Verknüpfungen
In diesem Beispiel sollen einige häufig genutzte Verknüpfungen von Ereignissen eingeführt werden. Wir wählen dazu für den Würfelwurf die Ereignisse A={3, 4}, B={4, 5} und C={6}. Man könnte nun etwa die Wahrscheinlichkeiten folgender verknüpfter Ereignisse ausrechnen:
A oder B:
A oder B oder C:
A und B (gleichzeitig):
Entweder A oder B (= A oder B, aber nicht A und B gleichzeitig):
Alternative Rechnung:
Hinweis: Die etwas kompliziertere Menge aus der alternativen Rechnung heißt soviel wie „jedes Elementarereignis aus A, das nicht in B ist oder jedes Elementarereignis aus B, das nicht in A ist”.
Weder A noch B:
Alternative Rechnung:
Die Regeln in der Übersicht (auswendig lernen muss man die nicht zwangsweise, wenn man das Prinzip hinter der Schnitt- und Vereinigungsmenge verstanden hat ergeben die sich von selbst):
- A oder B: P(A ∪ B)
- A und B (gleichzeitig): P(A ∩ B)
- Entweder A oder B:
- Weder A noch B:
- Höchstens eines (gar nichts oder A oder B aber nicht A und B gleichzeitig):
4. Summenregel
Eine weitere wichtige Regel ist die sogenannte Summenregel. Es gilt:
Übersetzt heißt das: Die Wahrscheinlichkeit von A oder B (P(A ∪ B)) ist identisch (=) mit der Wahrscheinlichkeit von A (P(A)) plus der Wahrscheinlichkeit von B (P(B)) minus der Wahrscheinlichkeit von A und gleichzeitig B (P(A ∩ B)).
Wieso muss P(A ∩ B) abgezogen werden? Das liegt daran, dass A und B gemeinsame Elementarereignisse enthalten können. Ist dies der Fall, dann würden die Wahrscheinlichkeiten dieser Elementarereignisse in P(A) sowie in P(B) berücksichtig und dadurch doppelt gezählt werden. Subtrahiert man aber P(A ∩ B), dann wird dieser Fehler korrigiert indem jede doppelt gezählte Wahrscheinlichkeit einmal abgezogen wird.
Nimmt man etwa beispielhaft an, dass gilt A=Ω und B=Ω, dann würde für P(A ∪ B) gelten P(Ω) + P(Ω) – P(Ω ∩ Ω) = 1 + 1 - 1 = 1. Ohne die Subtraktion von P(A ∩ B) hingegen: P(Ω) + P(Ω) = 2.
Nutzen der Summenformel: Es kann vorkommen, dass eine der beiden Seiten der Gleichung deutlich einfacher zu rechnen ist als die andere. In diesen Fällen spart man sich durch die Anwendung der Summenformel viel Zeit ein.
Ein weiterer Nutzen ist, dass man zur Bestimmung von Wahrscheinlichkeiten nicht mehr zwangsweise die Mengen der Ereignisse kennen muss. Sind stattdessen etwa die Werte von P(A), P(B) und P(A ∩ B) bekannt, dann kann P(A ∪ B) aus diesen abgeleitet werden.
5. Unvereinbare Ereignisse
Zwei Ereignisse gelten als unvereinbar, wenn ihre Schnittmenge die leere Menge ist: A ∩ B = ∅ → A und B sind unvereinbar
Wenn zwei Ereignisse unvereinbar sind, dann können sie nie gleichzeitig eintreten, denn beide Ereignisse haben dann kein einziges gemeinsames Elementarereignis.
Beispiel: Definieren wir für den Würfelwurf Agerade={2, 4, 6} und Bungerade={1, 3, 5}, dann gilt für Agerade ∩ Bungerade = ∅. Agerade und Bungerade haben keine gemeinsamen Elementarereignisse und können daher nicht gleichzeitig eintreten. Anders ausgedrückt: Man kann nicht gleichzeitig eine gerade und eine ungerade Augenzahl würfeln.
6. Quiz
Seien A und B Ereignisse, wie lässt sich dann P(A ∪ B) auch schreiben?
P(A) + P(B) + P(A ∩ B)
P(A) + P(B) - P(A ∪ B)
P(A) + P(B) - P(A ∩ B)
P(A) + P(B)
Seien A und B Ereignisse, welche der nachfolgenden Formeln repräsentiert dann die Wahrscheinlichkeit von A oder B?
P(A ∩ B)
P(A ∪ B)
P(A) – P(B) – P(A ∪ B)
P(A) + P(B)
Seien A und B Ereignisse, was drückt dann vereinfacht die nachfolgende Formel aus: P(A ∪ (B ∩ ∅) ∩ (A ∪ A))?
P(B)
P(A)
P(A ∩ B)
P(A ∪ B)
Seien A, B und C Ereignisse, welche der nachfolgenden Formeln drückt dann nicht die Wahrscheinlichkeit von „A oder B oder A und C gleichzeitig” aus?
P(A ∪ B ∪ (A ∩ C))
P((A ∩ B) ∪ C)
P(A ∪ (A ∩ C ∩ A) ∪ B ∪ A)
P((C ∩ A) ∪ A ∪ B ∪ ∅)