Schnellübersicht
Als bedingte Wahrscheinlichkeit wird die Wahrscheinlichkeit bezeichnet, dass das Ereignis A eintritt, wenn auch B eingetreten ist. Die Schreibweise lautet P(A|B) (gesprochen: P von A unter der Bedingung B). Das Ereignis, das zunächst erfüllt sein muss steht in dieser Schreibweise also am Ende (bzw. hinter dem senkrechten Strich). Will man es stattdessen am Anfang haben, dann kann man auch PB(A) schreiben. Letztere Schreibweise macht die „Reihenfolge” des Eintretens der Ereignisse klarer, allerdings kann das B auch leicht mit einem normalen Index verwechselt werden, daher wird sie seltener verwendet. Manchmal schreibt man für die gängigere Formel auch P(B|A), um für diese die Reihenfolge zu unterstreichen.
P(A|B) lässt sich vereinfacht wie folgt übersetzen: „Die Wahrscheinlichkeit, dass A eintritt, wenn zuvor B eingetreten ist.”
Die bedingte Wahrscheinlichkeit wird über die nachfolgende Formel ermittelt:
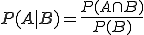 .
.
Wird stattdessen P(B|A) geschrieben, dann lautet die Formel entsprechend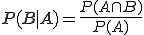 — wichtig ist nur sich zu merken, dass immer der Teil hinter dem senkrechten Strich (also die Bedingung) den Nenner des Bruchs bildet:
— wichtig ist nur sich zu merken, dass immer der Teil hinter dem senkrechten Strich (also die Bedingung) den Nenner des Bruchs bildet:
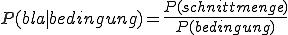
Die Formel kann umgestellt werden zu
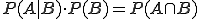 .
.
Zur Bestimmung der bedingten Wahrscheinlichkeit muss also immer die Wahrscheinlichkeit von A und die Wahrscheinlichkeit, dass A und B gleichzeitig eintreten, bekannt sein. Ist hingegen beispielsweise durch die Aufgabenstellung P(A|B) und P(A ∩ B) bekannt, dann lässt sich leicht P(B) bestimmten (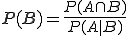 ).
).
Die größte Schwierigkeit bei der Anwendung der bedingten Wahrscheinlichkeit ist es, diese von der Schnittmenge zu unterscheiden, also P(A|B) vs. P(A ∩ B). Die Aufgabenstellungen für beide Wahrscheinlichkeiten klingen in der Regel sehr ähnlich und enthalten immer zwei Ereignisse oder Merkmale die „gleichzeitig” eintreten müssen. P(A ∩ B) lässt sich meist gut daran erkennen, dass das Wort und in Verbindung mit der Wahrscheinlichkeit verwendet wird (zur Erinnerung: die Schnittmenge wird auch als logische und-Verknüpfung bezeichnet).
Wichtig ist zu verstehen, dass P(A ∩ B) und P(B|A) unterschiedliche Wahrscheinlichkeiten sind. P(A ∩ B) bezeichnet die Wahrscheinlichkeit, dass man mit allen möglichen Ausgängen des Zufallsexperiments startet, dann zuerst das Ereignis A und dann auch noch das Ereignis B erhält. Bei P(B|A) ist bereits A eingetreten, die möglichen Ausgänge des Zufallsexperiments sind daher schon stark eingeschränkt. Nun wollen wir nur noch wissen, mit welcher Wahrscheinlichkeit jetzt wiederum B eintritt.
Angenommen die Massive Snort Biotech Corporation verkauft bisher ein beliebtes Anti-Grippe-Medikament. Sie ergänzt nun ihre Produktpalette mit einem Grippeschnelltest, der innerhalb von fünf Minuten ermitteln soll, ob jemand an Grippe erkrankt ist. In groß angelegten Studien hat Massive Snort Biotech herausgefunden, dass zum einen 5% der Bevölkerung zu einem beliebigen Zeitpunkt an Grippe erkrankt sind und zum anderen, dass die Wahrscheinlichkeit, dass eine einzelne Person an Grippe erkrankt ist und dies gleichzeitig durch den Schnelltest erfolgreich nachgewiesen wird bei 4,95% liegt. Wie zuverlässig erkennt der Schnelltest die Grippe bei bereits infizierten Personen? Wie hoch ist die Wahrscheinlichkeit, dass jemand an Grippe erkrankt ist und dies durch den Test nicht nachgewiesen wird?
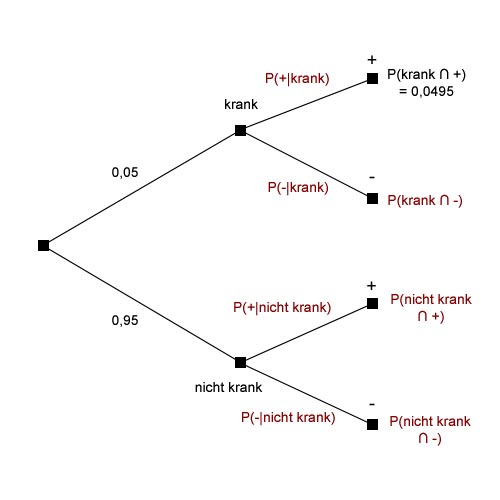
Lösung: Die Aufgabe kann als mehrstufiges Zufallsexperiment interpretiert werden. Im ersten Schritt wird bestimmt, ob eine Person krank oder nicht krank (P(krank) = 0,05, P(nicht krank)=0,95). Im zweiten Schritt wird bestimmt, ob der Schnelltest die Krankheit nachweist (hier mit + für positiv und - für negativ gekennzeichnet: P(+)=?, P(-)=?). Bekannt ist, dass gilt P(krank ∩ +)=0,0495. Gesucht sind P(+|krank) und P(krank ∩ -). Die Abbildung zeigt das passende Baumdiagramm:
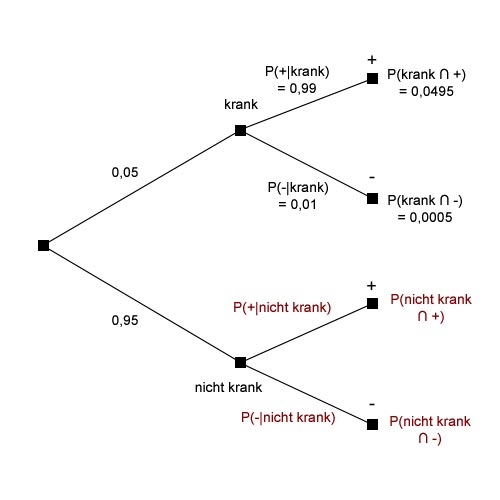
Wir ermitteln nun P(+|krank):
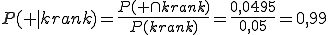 .
.
Die Wahrscheinlichkeit, dass der Schnelltest bei einer infizierten Person ein positives Ergebnis zurückgibt und dieses auch tatsächlich korrekt ist, beträgt 0,99 bzw. 99%.
Um nun P(krank ∩ -) zu bestimmen benötigen wird zunächst P(-|krank). Da der Baum an dieser Stelle nur zwei Abzweigungen hat stellt P(-|krank) das Gegenereignis zu P(+|krank) dar. Ihre Wahrscheinlichkeiten müssen sich also zu 1 summieren und es gilt P(-|krank) = 1 - P(+|krank) = 1 - 0,99 = 0,01 (bzw. 1%). Nun kann P(krank ∩ -) errechnet werden:
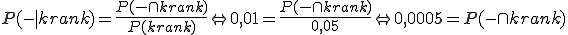 .
.
Die Wahrscheinlichkeit, dass eine beliebige Person krank ist und der Test gleichzeitig kein positives Resultat ergibt liegt also bei 0,05%.
Der Satz der totalen Wahrscheinlichkeit ist ein Hilfsmittel, um mit Hilfe von bekannten Wahrscheinlichkeiten weitere zu ermitteln. Er lautet:
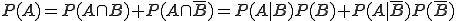
Beispiel: Das vorherige Beispiel soll fortgeführt werden. Die Statistiker von Massive Snort Biotech haben sich durch die ersten Rückmeldungen von Ärzten, Apotheken und Patienten gekämpft und sind zu dem Schluss gekommen, dass der Schnelltest bei etwa 19,7% aller nicht an Grippe erkrankten Personen fälschlicherweise eine Grippeerkrankung meldet.
Wie hoch ist die Wahrscheinlichkeit. dass eine nicht an Grippe erkrankte Person ein negatives Resultat erhält?
Wie hoch ist die Wahrscheinlichkeit, dass eine beliebige Person nicht an Grippe erkrankt ist und der Test korrekterweise ein negatives Resultat ergibt?
Wie hoch ist die Wahrscheinlichkeit, dass eine beliebige Person ein positives Resultat erhält?
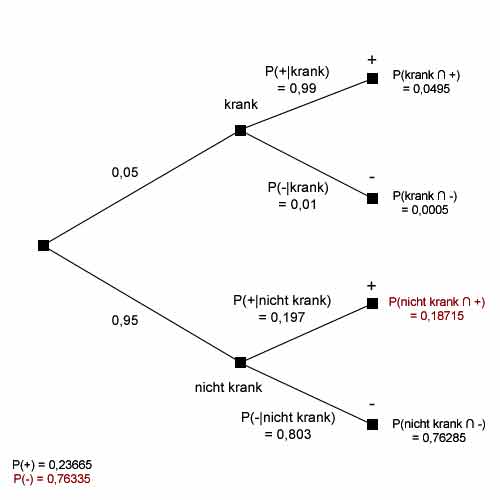
Die Abbildung zeigt alle bisher ermittelten Wert.
Lösung: Der neu hinzugekommene Wert lautet P(+|nicht krank)=0,197.
Frage 1) Hierbei handelt es sich um die bedingte Wahrscheinlichkeit P(-|nicht krank), die das Gegenereignis zu P(+|nicht krank) darstellt: P(-|nicht krank) = 1 – P(+|nicht krank) = 1 – 0,197 = 0,803.
Frage 2) Diese Frage lässt sich anhand der bekannten Wahrscheinlichkeiten P(nicht krank) und P(-|nicht krank) beantworten: P(nicht krank ∩ -) = P(nicht krank)*P(-|nicht krank) = 0,95*0,803 = 0,76285.
Frage 3) Zunächst Hierfür wird nun der Satz der totalen Wahrscheinlichkeit benötigt: P(+) = P(+|krank)P(krank) + P(+|nicht krank)P(nicht krank) = 0,99*0,05 + 0,197*0,95 = 0,23665.
Insgesamt erhalten also mehr als 23% aller Anwender vom Test die Rückmeldung, dass sie krank sind, obwohl dies tatsächlich nur auf 5% zutrifft. Die neuen Werten sind in der Abbildung unten eingetragen (sowie zusätzlich P(nicht krank ∩ +) und P(-)).
Im Vergleich zum Rechenaufwand ist die Herleitung der bedingten Wahrscheinlichkeit recht einfach. Schauen wir uns dafür noch mal die Beispielgrafiken vom Anfang an, welche eine Zufallsexperiment zeigen bei dem es im ersten Schritt die Möglichkeiten A und nicht-A, im zweiten dann die Möglichkeiten B und nicht-B gibt.
Rot gekennzeichnet ist der Pfad auf den wir uns konzentrieren. Es gibt die Wahrscheinlichkeiten
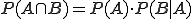 (Pfad = erster Abschnitt * zweiter Abschnitt).
(Pfad = erster Abschnitt * zweiter Abschnitt).
Und genau das lässt sich jetzt durch eine einfache Division umstellen zu:
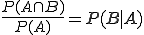 ,
,
was der Formel für die bedingte Wahrscheinlichkeit entspricht.
- Die Wahrscheinlichkeit, dass das Ereignis A eintritt unter der Bedingung, dass auch B eintritt wird als bedingte Wahrscheinlichkeit bezeichnet und P(A|B) geschrieben.
- Die Formel für die bedingte Wahrscheinlichkeit lautet
. Je nachdem welche Werte bekannt sind können über diese Formel auch P(A ∩ B) und P(B) ermittelt werden.
- P(A|B) heißt, dass zuerst B eingetreten ist und nun bestimmt werden soll, wie hoch die Wahrscheinlichkeit ist, dass dann auch noch A eintritt.
- P(A|B) und P(A ∩ B) sind sehr ähnlich, dürfen aber nicht miteinander verwechselt werden. P(A|B) kann als Teil von P(A ∩ B) interpretiert werden.
- Der Satz der totalen Wahrscheinlichkeit lautet
.
1. Einleitung
Als bedingte Wahrscheinlichkeit wird die Wahrscheinlichkeit bezeichnet, dass das Ereignis A eintritt, wenn auch B eingetreten ist. Die Schreibweise lautet P(A|B) (gesprochen: P von A unter der Bedingung B). Das Ereignis, das zunächst erfüllt sein muss steht in dieser Schreibweise also am Ende (bzw. hinter dem senkrechten Strich). Will man es stattdessen am Anfang haben, dann kann man auch PB(A) schreiben. Letztere Schreibweise macht die „Reihenfolge” des Eintretens der Ereignisse klarer, allerdings kann das B auch leicht mit einem normalen Index verwechselt werden, daher wird sie seltener verwendet. Manchmal schreibt man für die gängigere Formel auch P(B|A), um für diese die Reihenfolge zu unterstreichen.
P(A|B) lässt sich vereinfacht wie folgt übersetzen: „Die Wahrscheinlichkeit, dass A eintritt, wenn zuvor B eingetreten ist.”
Die bedingte Wahrscheinlichkeit wird über die nachfolgende Formel ermittelt:
Wird stattdessen P(B|A) geschrieben, dann lautet die Formel entsprechend
Die Formel kann umgestellt werden zu
Zur Bestimmung der bedingten Wahrscheinlichkeit muss also immer die Wahrscheinlichkeit von A und die Wahrscheinlichkeit, dass A und B gleichzeitig eintreten, bekannt sein. Ist hingegen beispielsweise durch die Aufgabenstellung P(A|B) und P(A ∩ B) bekannt, dann lässt sich leicht P(B) bestimmten (
1.1. Erkennung der bedingten Wahrscheinlichkeit
Die größte Schwierigkeit bei der Anwendung der bedingten Wahrscheinlichkeit ist es, diese von der Schnittmenge zu unterscheiden, also P(A|B) vs. P(A ∩ B). Die Aufgabenstellungen für beide Wahrscheinlichkeiten klingen in der Regel sehr ähnlich und enthalten immer zwei Ereignisse oder Merkmale die „gleichzeitig” eintreten müssen. P(A ∩ B) lässt sich meist gut daran erkennen, dass das Wort und in Verbindung mit der Wahrscheinlichkeit verwendet wird (zur Erinnerung: die Schnittmenge wird auch als logische und-Verknüpfung bezeichnet).
1.2. Unterschied zwischen Schnittmenge und bedingter Wahrscheinlichkeit
Wichtig ist zu verstehen, dass P(A ∩ B) und P(B|A) unterschiedliche Wahrscheinlichkeiten sind. P(A ∩ B) bezeichnet die Wahrscheinlichkeit, dass man mit allen möglichen Ausgängen des Zufallsexperiments startet, dann zuerst das Ereignis A und dann auch noch das Ereignis B erhält. Bei P(B|A) ist bereits A eingetreten, die möglichen Ausgänge des Zufallsexperiments sind daher schon stark eingeschränkt. Nun wollen wir nur noch wissen, mit welcher Wahrscheinlichkeit jetzt wiederum B eintritt.
P(A ∩ B) am Beispiel eines Baumdiagramms
2. Beispiel
Angenommen die Massive Snort Biotech Corporation verkauft bisher ein beliebtes Anti-Grippe-Medikament. Sie ergänzt nun ihre Produktpalette mit einem Grippeschnelltest, der innerhalb von fünf Minuten ermitteln soll, ob jemand an Grippe erkrankt ist. In groß angelegten Studien hat Massive Snort Biotech herausgefunden, dass zum einen 5% der Bevölkerung zu einem beliebigen Zeitpunkt an Grippe erkrankt sind und zum anderen, dass die Wahrscheinlichkeit, dass eine einzelne Person an Grippe erkrankt ist und dies gleichzeitig durch den Schnelltest erfolgreich nachgewiesen wird bei 4,95% liegt. Wie zuverlässig erkennt der Schnelltest die Grippe bei bereits infizierten Personen? Wie hoch ist die Wahrscheinlichkeit, dass jemand an Grippe erkrankt ist und dies durch den Test nicht nachgewiesen wird?
Lösung: Die Aufgabe kann als mehrstufiges Zufallsexperiment interpretiert werden. Im ersten Schritt wird bestimmt, ob eine Person krank oder nicht krank (P(krank) = 0,05, P(nicht krank)=0,95). Im zweiten Schritt wird bestimmt, ob der Schnelltest die Krankheit nachweist (hier mit + für positiv und - für negativ gekennzeichnet: P(+)=?, P(-)=?). Bekannt ist, dass gilt P(krank ∩ +)=0,0495. Gesucht sind P(+|krank) und P(krank ∩ -). Die Abbildung zeigt das passende Baumdiagramm:
Die Wahrscheinlichkeit, dass der Schnelltest bei einer infizierten Person ein positives Ergebnis zurückgibt und dieses auch tatsächlich korrekt ist, beträgt 0,99 bzw. 99%.
Um nun P(krank ∩ -) zu bestimmen benötigen wird zunächst P(-|krank). Da der Baum an dieser Stelle nur zwei Abzweigungen hat stellt P(-|krank) das Gegenereignis zu P(+|krank) dar. Ihre Wahrscheinlichkeiten müssen sich also zu 1 summieren und es gilt P(-|krank) = 1 - P(+|krank) = 1 - 0,99 = 0,01 (bzw. 1%). Nun kann P(krank ∩ -) errechnet werden:
Die Wahrscheinlichkeit, dass eine beliebige Person krank ist und der Test gleichzeitig kein positives Resultat ergibt liegt also bei 0,05%.
3. Satz der totalen Wahrscheinlichkeit
Der Satz der totalen Wahrscheinlichkeit ist ein Hilfsmittel, um mit Hilfe von bekannten Wahrscheinlichkeiten weitere zu ermitteln. Er lautet:
Beispiel: Das vorherige Beispiel soll fortgeführt werden. Die Statistiker von Massive Snort Biotech haben sich durch die ersten Rückmeldungen von Ärzten, Apotheken und Patienten gekämpft und sind zu dem Schluss gekommen, dass der Schnelltest bei etwa 19,7% aller nicht an Grippe erkrankten Personen fälschlicherweise eine Grippeerkrankung meldet.
Wie hoch ist die Wahrscheinlichkeit. dass eine nicht an Grippe erkrankte Person ein negatives Resultat erhält?
Wie hoch ist die Wahrscheinlichkeit, dass eine beliebige Person nicht an Grippe erkrankt ist und der Test korrekterweise ein negatives Resultat ergibt?
Wie hoch ist die Wahrscheinlichkeit, dass eine beliebige Person ein positives Resultat erhält?
Die Abbildung zeigt alle bisher ermittelten Wert.
Lösung: Der neu hinzugekommene Wert lautet P(+|nicht krank)=0,197.
Frage 1) Hierbei handelt es sich um die bedingte Wahrscheinlichkeit P(-|nicht krank), die das Gegenereignis zu P(+|nicht krank) darstellt: P(-|nicht krank) = 1 – P(+|nicht krank) = 1 – 0,197 = 0,803.
Frage 2) Diese Frage lässt sich anhand der bekannten Wahrscheinlichkeiten P(nicht krank) und P(-|nicht krank) beantworten: P(nicht krank ∩ -) = P(nicht krank)*P(-|nicht krank) = 0,95*0,803 = 0,76285.
Frage 3) Zunächst Hierfür wird nun der Satz der totalen Wahrscheinlichkeit benötigt: P(+) = P(+|krank)P(krank) + P(+|nicht krank)P(nicht krank) = 0,99*0,05 + 0,197*0,95 = 0,23665.
Insgesamt erhalten also mehr als 23% aller Anwender vom Test die Rückmeldung, dass sie krank sind, obwohl dies tatsächlich nur auf 5% zutrifft. Die neuen Werten sind in der Abbildung unten eingetragen (sowie zusätzlich P(nicht krank ∩ +) und P(-)).
4. Herleitung
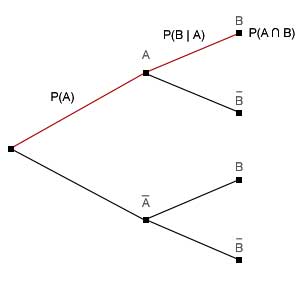
Im Vergleich zum Rechenaufwand ist die Herleitung der bedingten Wahrscheinlichkeit recht einfach. Schauen wir uns dafür noch mal die Beispielgrafiken vom Anfang an, welche eine Zufallsexperiment zeigen bei dem es im ersten Schritt die Möglichkeiten A und nicht-A, im zweiten dann die Möglichkeiten B und nicht-B gibt.
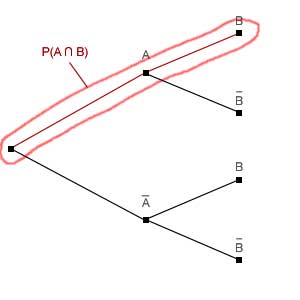
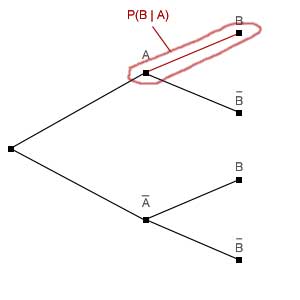
Rot gekennzeichnet ist der Pfad auf den wir uns konzentrieren. Es gibt die Wahrscheinlichkeiten
- P(A): Die Wahrscheinlichkeit, dass im ersten Schritt A eintritt (statt nicht-A)
- P(B|A): Die Wahrscheinlichkeit, dass im zweiten Schritt B eintritt (statt nicht-B, vorausgesetzt im ersten Schritt ist A eingetreten).
- P(A ∩ B): Die Wahrscheinlichkeit, dass im ersten Schritt A und im zweiten Schritt B eintritt.
Und genau das lässt sich jetzt durch eine einfache Division umstellen zu:
was der Formel für die bedingte Wahrscheinlichkeit entspricht.
Kommentare (3)
Von neu nach altWir bitten um ihr Verständnis.
Ich versuche das jetzt aufzufrischen und muß sagen, das ganze Skript ist großartig.