Druckversion: Binomialverteilung (Stochastik)

1. Definition der Binomialverteilung

Stellen wir uns vor, dass wir ein Zufallsexperiment haben. Wir werden dieses Zufallsexperiment n mal wiederholen. Wir hoffen nun, dass ein ganz bestimmtes Ereignis eintritt — und zwar nicht beliebig oft, sondern exakt x mal (natürlich sollte x kleiner als n sein, sonst wird das schwierig...). Wir wissen zudem, dass das Ereignis mit einer Wahrscheinlichkeit p eintreten wird und dass sich diese Wahrscheinlichkeit nicht ändern wird, egal wie oft wir das Experiment wiederholen (so wie beim Münzwurf jede Seite immer die gleiche Wahrscheinlichkeit hat, egal wie oft man wirft). Wie hoch ist nun die Wahrscheinlichkeit, dass wir das Ereignis exakt besagte x mal erhalten werden?
Zusammengefasst: Wir haben n Wiederholungen. Das Ereignis tritt mit der Wahrscheinlichkeit p ein (welche sich nicht verändert). Wir wollen wissen, mit welcher Wahrscheinlichkeit es x mal eintreten wird.
Dies ist eine Situation in der die sogenannte Binomialverteilung angewendet werden kann. Ihre Formel lautet:

$Formel-Code: B(x|n; p) = \left( \begin{array} n \\ x \end{array} \right) p^x (1-p)^{n-x}$

In dieser Formel ist $Formel-Code: \left( \begin{array} n \\ x \end{array} \right)$ der sogenannte Binomialkoeffizient (nach dem die Binomialverteilung benannt wurde). Er wird im Artikel zur Kombination (Thema Kombinatorik) genauer beschrieben. Die meisten Taschenrechner bieten eine eigene Taste an, um den Wert des Binomialkoeffizienten zu errechnen. Dies ist häufig nCr. Die Eingabe würde dann lauten: n, nCr, x, = (wobei n und x logischerweise Zahlen sind).

2. Beispiel

Angenommen wir haben eine Katze, die bald Jungtiere austragen wird. Wir schätzen die Zahl der Jungtiere auf voraussichtlich 8. Wir wissen zudem, dass jedes Jungtier mit einer Wahrscheinlichkeit von exakt 50% weiblich ist (und entsprechend umgekehrt mit 50%iger Wahrscheinlichkeit männlich).


Anteil	50%	50%

Uns interessiert nun: Wie hoch ist die Wahrscheinlichkeit, dass der Wurf exakt 4 weibliche Kätzchen enthalten wird?
Lösung: Die Werte sind n=8 (da voraussichtlich acht Jungtiere), x=4 (da wir auf 4 weibliche Katzen testen) und p=0,5 (da weibliche und männliche Katzen beide eine Wahrscheinlichkeit von 50%) haben. In die Formel eingesetzt lautet das:

$Formel-Code: B(x|n; p) = B(4|8; 0,5) = \left( \begin{array} 8 \\ 4 \end{array} \right) 0,5^4 (1-0,5)^{8-4} = \left( \begin{array} 8 \\ 4 \end{array} \right) 0,5^4 \cdot 0,5^{4} = 70 \cdot \frac{1}{256} \approx 0,2734$

Die Wahrscheinlichkeit, dass der Wurf exakt 4 weibliche und 4 männliche Katzen enthalten wird liegt also bei etwa 27,34%.

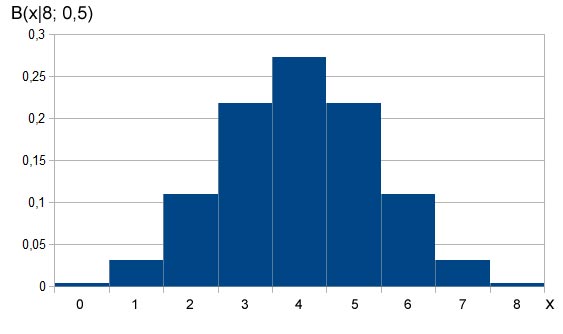
Berechnen wir zudem noch die Wahrscheinlichkeiten der anderen Verteilungen von männlichen und weiblichen Kätzchen:

Anzahl	Wahrscheinlichkeit
0 weibliche Kätzchen	$Formel-Code: B(0\|8; 0,5) = \left( \begin{array} 8 \\ 0 \end{array} \right) 0,5^0 (1-0,5)^{8-0} = 1 \cdot 1 \cdot 0,5^8 = \frac{1}{256} \approx 0,0039$
1 weibliches Kätzchen	$Formel-Code: B(1\|8; 0,5) = \left( \begin{array} 8 \\ 1 \end{array} \right) 0,5^1 (1-0,5)^{8-1} = 8 \cdot 0,5 \cdot 0,5^7 = \frac{1}{32} \approx 0,03125$
2 weibliche Kätzchen	$Formel-Code: B(2\|8; 0,5) = \left( \begin{array} 8 \\ 2 \end{array} \right) 0,5^2 (1-0,5)^{8-2} = 28 \cdot \frac{1}{4} \cdot 0,5^6 = \frac{7}{64} \approx 0,1094$
3 weibliche Kätzchen	$Formel-Code: B(3\|8; 0,5) = \left( \begin{array} 8 \\ 3 \end{array} \right) 0,5^3 (1-0,5)^{8-3} = 56 \cdot \frac{1}{8} \cdot 0,5^5 = \frac{7}{32} \approx 0,2188$
4 weibliche Kätzchen	$Formel-Code: B(4\|8; 0,5) = \frac{70}{256} \approx 0,2734$ (bereits oben berechnet)
5 weibliche Kätzchen	$Formel-Code: B(5\|8; 0,5) = \left( \begin{array} 8 \\ 5 \end{array} \right) 0,5^5 (1-0,5)^{8-5} = 56 \cdot \frac{1}{32} \cdot 0,5^3 = \frac{7}{32} \approx 0,2188$
6 weibliche Kätzchen	$Formel-Code: B(6\|8; 0,5) = \left( \begin{array} 8 \\ 6 \end{array} \right) 0,5^6 (1-0,5)^{8-6} = 28 \cdot \frac{1}{64} \cdot 0,5^2 = \frac{7}{64} \approx 0,1094$
7 weibliche Kätzchen	$Formel-Code: B(7\|8; 0,5) = \left( \begin{array} 8 \\ 7 \end{array} \right) 0,5^7 (1-0,5)^{8-7} = 8 \cdot \frac{1}{128} \cdot 0,5 = \frac{1}{32} \approx 0,03125$
8 weibliche Kätzchen	$Formel-Code: B(8\|8; 0,5) = \left( \begin{array} 8 \\ 8 \end{array} \right) 0,5^8 (1-0,5)^{8-8} = 1 \cdot \frac{1}{256} \cdot 1 = \frac{1}{256} \approx 0,0039$

Die Wahrscheinlichkeitsverteilung hat also hier die Form eines Dachs. Sie steigt zu X=4 hin an und erreicht dort ihren Hochpunkt. Danach fällt sie genauso wieder ab. Aus diesen Zahlen können wir z. B. auch ermitteln, dass die Wahrscheinlichkeit von 3 bis 5 weiblichen Katzen (oder 3 bis 5 männlichen Katzen) im Wurf folgenden Wert hat:

$Formel-Code: P(3 \leq X \leq 5) = P(X=3) + P(X=4) + P(X=5) = \frac{7}{32} + \frac{70}{256} + \frac{7}{32} = \frac{91}{128} \approx 0,711$

Wir können also mit einer Wahrscheinlichkeit von 71,1% davon ausgehen, dass drei bis fünf weibliche Katzen im Wurf sein werden.

Histogramm zu den erhaltenen Wahrscheinlichkeiten

3. Erwartungswert

Der Erwartungswert der Binomialverteilung ist simpel zu berechnen, er lautet schlicht:

(Wenn man zu viel Zeit hat kann man den Erwartungswert natürlich auch über den normalen Weg berechnen und jeden Wert der Zufallsvariable mit der zugehörige Wahrscheinlichkeit multiplizieren.)
Für das vorherige Katzenbeispiel (n=8, p=0,5) ist der Erwartungswert demnach:

$Formel-Code: E(X) = np = 8 \cdot 0,5 = 4$

Der Erwartungswert liegt also genau in dem Bereich, den wir bereits als Hochpunkt der Verteilung ermittelt haben.
Bei der Gelegenheit können wir prüfen, wie sich der Erwartungswert bei anderen Werten für n und p verändert. Prüfen wir zunächst andere Werte für n (p=0,5):

Bei n=1: E(X) = 1*0,5 = 0,5
Bei n=2: E(X) = 2*0,5 = 1
Bei n=4: E(X) = 4*0,5 = 2
Bei n=8: E(X) = 8*0,5 = 4
Bei n=16: E(X) = 16*0,5 = 8

Da sich die Anzahl der Katzen im Wurf (n) ändert, aber nicht die Wahrscheinlichkeit (p) wird die Wahrscheinlichkeitsverteilung „breiter”. Der Erwartungswert bleibt jeweils in der Mitte zwischen den Extremwerten (0 weibliche Katzen und n weibliche Katzen).

Bei anderem p (n=8):

Bei p=0,05: E(X) = 8*0,05 = 0,4
Bei p=0,25: E(X) = 8*0,25 = 2,0
Bei p=0,45: E(X) = 8*0,45 = 3,6
Bei p=0,50: E(X) = 8*0,50 = 4,0
Bei p=0,55: E(X) = 8*0,55 = 4,4
Bei p=0,75: E(X) = 8*0,75 = 6,0
Bei p=0,95: E(X) = 8*0,95 = 7,6

Wird die Wahrscheinlichkeit verändert, dann verändert sich auch die Form der Verteilung. Statt einem Dach ähnelt sie dann eher einer Welle, welche ihre Spitze bei niedrigen X-Werten (p<0,5) oder bei hohen X-Werten (p>0,5) haben kann.

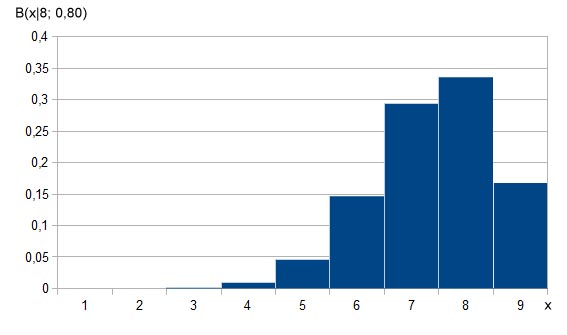
Eine Binomialverteilung mit n=8 und p=0,8 hätte z. B. das nachfolgende Aussehen:

Histogramm für Binomialverteilung mit p=0,8 und n=8

Die Werte dieser Binomialverteilung lauten wie folgt:

x	0	1	2	3	4	5	6	7	8
B(x\|8; 0,80)	0,00000256	0,00008192	0,00114688	0,00917504	0,04587520	0,14680064	0,29360128	0,33554432	0,16777216

4. Varianz und Standardabweichung

Auch die Varianz lässt sich bei der Binomialverteilung vergleichsweise leicht bestimmen. Die Formel lautet

$Formel-Code: Var(X) = n \cdot p \cdot (1-p)$

Die Standardabweichung lässt sich entsprechend wieder über $Formel-Code: \sigma = \sqrt{Var(X)}$ bestimmen.
Berechnet man die Varianz zum obigen Katzenbeispiel bei n=8, x=4 und p=0,5, dann ergibt sich folgender Wert:

$Formel-Code: Var(X) = 8 \cdot 0,5 \cdot (1-0,5) = 2$

Verwendet man hingegen eine Wahrscheinlichkeit von p=0,01 dann liegt die Varianz bei

$Formel-Code: Var(X) = 8 \cdot 0,01 \cdot (0,99) = 0,0792$

Die Varianz verringert sich also deutlich, wenn p von 0,5 abweicht. Bezogen auf das Beispiel heißt das, dass bei niedrigem p auch nur noch sehr selten weibliche Katzen geboren werden. Entsprechend wird es immer wahrscheinlicher, dass ein Wert von 0 weiblichen Katzen erreicht wird , wodurch es zu immer weniger Schwankungen kommt (je niedriger p ist). Liegt p hingegen nahe 0,5, gibt es mehrere realistische Möglichkeiten neben 4 weiblichen Katzen (z. B. 3 weibliche Katzen oder 5 weibliche). Entsprechend ist die Varianz höher.