Schnellübersicht
Die Kombination ist sehr ähnlich zur Variation. Der einzige Unterschied ist, dass die genauen Reihenfolgen der Anordnungen keine Rolle spielen (ohne Beachtung der Reihenfolge), stattdessen wird die Anzahl der verschiedenen Kombinationen von Elementen gezählt (daher auch der Name). Angenommen wir haben etwa die Buchstaben A, B, C, D (n=4) und wählen aus diesen 3 ohne Zurücklegen aus, dann ergeben sich folgende „Blöcke” von verschiedenen Anordnungen (insgesamt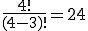 mögliche Anordnungen, siehe Variation):
mögliche Anordnungen, siehe Variation):
Die Formel für die Kombination ist ebenfalls ähnlich zu der der Variation. Der Bruch wird allerdings zusätzlich durch k! geteilt (denn es gibt (fast) immer weniger Kombinationen als verschiedene Anordnungen). Die Anzahl der Kombinationen lässt sich nun bei n Elementen von denen k ausgewählt werden sollen wie folgt berechnen:
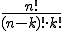 Für diesen Bruch gibt es eine besondere Schreibweise:
Für diesen Bruch gibt es eine besondere Schreibweise:
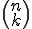 Man bezeichnet diese Schreibweise als Binomialkoeffizient und sagt: „n über k”. Der Binomialkoeffizient ist kein Vektor! Er ist nur eine andere (kürzere) Schreibweise für die zuvor genannte Formel. Es gilt also
Man bezeichnet diese Schreibweise als Binomialkoeffizient und sagt: „n über k”. Der Binomialkoeffizient ist kein Vektor! Er ist nur eine andere (kürzere) Schreibweise für die zuvor genannte Formel. Es gilt also
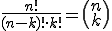
Den Binomialkoeffizienten muss man nicht selber ausrechnen. Jeder halbwegs moderne Taschenrechner sollte eine Taste dafür besitzen. Diese heißt zumeist nCr, wobei das n (nCr) für die Anzahl der Elemente (n) und C (nCr) für „Combinations” steht. Das k wiederum wird durch r (nCr) repräsentiert. Entsprechend fällt die Reihenfolge in der die Tasten gedrückt werden aus, falls z. B. n=8 und k=4 ist: 8 (n), shift, nCr, 4 (k), = (ob eine shift-Taste gedrückt werden muss und wie die dann genau heißt hängt vom Taschenrechner ab).
Also merken: das C steht für Combinations (recht wichtig, denn es gibt häufig auch eine nPr-Taste) und das „nCr” verrät schon, dass zuerst das n und danach das k eingegeben werden muss.
Falls der eigene Taschenrechner keine Taste für den Binomialkoeffizienten bietet (ein Blick in die Anleitung oder eine Google-Suche nach „<Taschenrechnermodell> Binomialkoeffizient” klärt auf), dann ist es sehr zu empfehlen, sich einen anzuschaffen der das kann. Andernfalls tritt schnell mal das Problem auf, dass der Taschenrechner die großen Zahlen im Bruch (die durch die Fakultäten entstehen) nicht mehr berechnen kann. Dann kann man evt. eine Aufgabe nicht lösen nur weil der Taschenrechner nicht mitmacht. (Wenn sowieso kein Taschenrechner bei der Klausur verwendet werden darf kann man sich das natürlich sparen.)
Das klassische Beispiel für die Kombination ist Lotto. Dabei werden von 49 Zahlen 6 verschiedene ausgewählt. Die Reihenfolge in der diese Zahlen ausgewählt werden spielt bei der Vergabge der Gewinne keine Rolle. Die Anzahl der Kombinationen errechnet sich wie folgt:
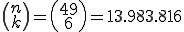 (49 über 6 im Taschenrechner: [4][9], [shift], [nCr], [6], [=])
(49 über 6 im Taschenrechner: [4][9], [shift], [nCr], [6], [=])
Da jede Kombination die selbe Wahrscheinlichkeit hat gezogen zu werden, beträgt die Wahrscheinlichkeit einer beliebigen Kombination aus sechs Zahlen: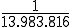 (das entspricht der Wahrscheinlichkeit, 6 richtige zu haben).
(das entspricht der Wahrscheinlichkeit, 6 richtige zu haben).
Die Wahrscheinlichkeit von sechs richtigen und zusätzlich einer richtig getippten Zusatzzahl ist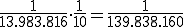 , denn es gibt zehn mögliche Zusatzzahlen, die alle mit der selben Wahrscheinlichkeit gezogen werden können.
, denn es gibt zehn mögliche Zusatzzahlen, die alle mit der selben Wahrscheinlichkeit gezogen werden können.
Bisher wurde die Kombination mit Ziehen ohne Zurücklegen besprochen. Soll ein Element auch mehrmals gezogen werden dürfen (Ziehen mit Zurücklegen), dann lautet die Formel wie folgt:
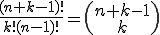 Es kommt also beim Binomialkoeffizienten ein +k-1 hinzu, ansonsten bleibt die Formel gleich.
Es kommt also beim Binomialkoeffizienten ein +k-1 hinzu, ansonsten bleibt die Formel gleich.
Beispiel: Angenommen die Lottozahlen würden mit der Methoden Ziehen mit Zurücklegen gezogen werden. Bei 49 Zahlen von denen 6 ausgewählt werden würde die Anzahl der möglichen Kombinationen auf folgenden Wert steigen:
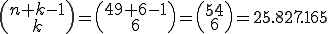 Die Wahrscheinlichkeit, sechs richtige zu erhalten würde dann bei
Die Wahrscheinlichkeit, sechs richtige zu erhalten würde dann bei 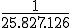 liegen (ohne Beachtung der Zusatzzahl).
liegen (ohne Beachtung der Zusatzzahl).

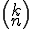
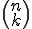
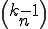
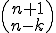


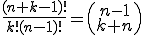
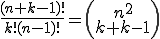
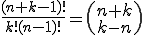
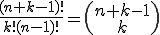
- Die Kombination ist ähnlich zur Variation.
- Aus n Elementen werden wieder k ausgewählt.
- Es werden diesmal die möglichen Kombinationen gezählt (statt: mögliche Anordnungen). Z. B. würden {A, B, C}, {A, C, B} und {C, A, B} drei verschiedene Anordnungen aber nur eine Kombination bilden.
- Die Formel lautet beim Ziehen ohne Zurücklegen:
wird als Binomialkoeffizient bezeichnet und gesprochen „n über k”. Jeder gute Taschenrechner hat in der Regel eine Taste für den Binomialkoeffizienten, häufig nCr (C wie Combinations).
- Die Formel für das Ziehen mit Zurücklegen lautet:
1. Einleitung: Unterschied zur Variation
Die Kombination ist sehr ähnlich zur Variation. Der einzige Unterschied ist, dass die genauen Reihenfolgen der Anordnungen keine Rolle spielen (ohne Beachtung der Reihenfolge), stattdessen wird die Anzahl der verschiedenen Kombinationen von Elementen gezählt (daher auch der Name). Angenommen wir haben etwa die Buchstaben A, B, C, D (n=4) und wählen aus diesen 3 ohne Zurücklegen aus, dann ergeben sich folgende „Blöcke” von verschiedenen Anordnungen (insgesamt
- für die Elemente A, B und C:
- A, B, C
- A, C, B
- B, A, C
- B, C, A
- C, A, B
- C, B, A
- für die Elemente A, B und D:
- A, B, D
- A, D, B
- B, A, D
- B, D, A
- D, A, B
- D, B, A
- für die Elemente A, C und D:
- A, C, D
- A, D, C
- C, A, D
- C, D, A
- D, A, C
- D, C, A
- für die Elemente B, C und D:
- B, C, D
- B, D, C
- C, B, D
- C, D, B
- D, B, C
- D, C, B
2. Berechnung und Binomialkoeffizient
Die Formel für die Kombination ist ebenfalls ähnlich zu der der Variation. Der Bruch wird allerdings zusätzlich durch k! geteilt (denn es gibt (fast) immer weniger Kombinationen als verschiedene Anordnungen). Die Anzahl der Kombinationen lässt sich nun bei n Elementen von denen k ausgewählt werden sollen wie folgt berechnen:
2.1. Binomialkoeffizient und Taschenrechner (nCr)
Den Binomialkoeffizienten muss man nicht selber ausrechnen. Jeder halbwegs moderne Taschenrechner sollte eine Taste dafür besitzen. Diese heißt zumeist nCr, wobei das n (nCr) für die Anzahl der Elemente (n) und C (nCr) für „Combinations” steht. Das k wiederum wird durch r (nCr) repräsentiert. Entsprechend fällt die Reihenfolge in der die Tasten gedrückt werden aus, falls z. B. n=8 und k=4 ist: 8 (n), shift, nCr, 4 (k), = (ob eine shift-Taste gedrückt werden muss und wie die dann genau heißt hängt vom Taschenrechner ab).
Also merken: das C steht für Combinations (recht wichtig, denn es gibt häufig auch eine nPr-Taste) und das „nCr” verrät schon, dass zuerst das n und danach das k eingegeben werden muss.
Falls der eigene Taschenrechner keine Taste für den Binomialkoeffizienten bietet (ein Blick in die Anleitung oder eine Google-Suche nach „<Taschenrechnermodell> Binomialkoeffizient” klärt auf), dann ist es sehr zu empfehlen, sich einen anzuschaffen der das kann. Andernfalls tritt schnell mal das Problem auf, dass der Taschenrechner die großen Zahlen im Bruch (die durch die Fakultäten entstehen) nicht mehr berechnen kann. Dann kann man evt. eine Aufgabe nicht lösen nur weil der Taschenrechner nicht mitmacht. (Wenn sowieso kein Taschenrechner bei der Klausur verwendet werden darf kann man sich das natürlich sparen.)
3. Beispiel
Das klassische Beispiel für die Kombination ist Lotto. Dabei werden von 49 Zahlen 6 verschiedene ausgewählt. Die Reihenfolge in der diese Zahlen ausgewählt werden spielt bei der Vergabge der Gewinne keine Rolle. Die Anzahl der Kombinationen errechnet sich wie folgt:
Da jede Kombination die selbe Wahrscheinlichkeit hat gezogen zu werden, beträgt die Wahrscheinlichkeit einer beliebigen Kombination aus sechs Zahlen:
Die Wahrscheinlichkeit von sechs richtigen und zusätzlich einer richtig getippten Zusatzzahl ist
4. Kombination mit Zurücklegen
Bisher wurde die Kombination mit Ziehen ohne Zurücklegen besprochen. Soll ein Element auch mehrmals gezogen werden dürfen (Ziehen mit Zurücklegen), dann lautet die Formel wie folgt:
Beispiel: Angenommen die Lottozahlen würden mit der Methoden Ziehen mit Zurücklegen gezogen werden. Bei 49 Zahlen von denen 6 ausgewählt werden würde die Anzahl der möglichen Kombinationen auf folgenden Wert steigen:
5. Quiz
Wie wird die Kombination ohne Zurücklegen bei n Elementen von denen k ausgewählt werden sollen gewöhnlich geschrieben?
Wie bezeichnet man 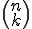 auch?
auch?
Wahrscheinlichkeitsfaktor
Tetrapotent
Vektorexponent
Binomialkoeffizient
Wie lautet die Formel für die Kombination mit Zurücklegen bei n Elementen von denen k ausgewählt werden sollen (inklusive alternativer Schreibweise)?
Kommentare (3)
Von neu nach altWir bitten um ihr Verständnis.
bzw. würde das Kapitel gut vervollständigen.