Schnellübersicht
Die hypergeometrische Verteilung ist sozusagen der Bruder der Binomialverteilung. Wir erinnern uns: bei der Binomialverteilung wurde berechnet wie hoch die Wahrscheinlichkeit ist, nach n Wiederholungen eines Experiments (bzw. nach n Zügen) exakt x Treffer erzielt zu haben. Die hypergeometrische Verteilung misst genau das selbe. Der einzige Unterschied ist nur, dass die Binomialverteilung davon ausgeht, dass sich die Wahrscheinlichkeit eines Treffers pro Zug nicht ändert. Sie funktioniert also nach dem Prinzip Ziehen mit Zurücklegen. Die hypergeometrische Verteilung hingegen geht davon aus, dass die Menge aus der gezogen wird begrenzt ist und dass alles was gezogen wurde nicht mehr zurückgelegt wird. Nach jedem Zug (bzw. nach jeder Wiederholung des Experiments) ändert sich also die Wahrscheinlichkeit.
Für die Formel müssen nun zuerst folgende Variablen definiert werden:
Die hypergeometrische Verteilung errechnet sich dann über:
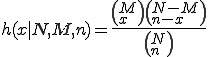 Wie bei der Binomialverteilung ist auch hier
Wie bei der Binomialverteilung ist auch hier 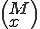 der Binomialkoeffizient und wird im Artikel zur Kombination beschrieben.
der Binomialkoeffizient und wird im Artikel zur Kombination beschrieben.
Angenommen das Unternehmen „Carne Malata International” (kurz: CMI) aus Neapel stellt sie als Statistiker ein. CMI ist ein Lieferant von äußerst preisgünstigem Intensivgeschmackfleisch, das die Darmflora aktiv anregt. Der ehrenwerte CEO beschreibt sein Unternehmen:
Zitat: CEO
Aus der Aufgabenstellung gehen folgende Variablen hervor:
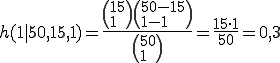 Das heißt, dass wir eine verunreinigte Fuhre mit einer Wahrscheinlichkeit von 30% erkennen.
Das heißt, dass wir eine verunreinigte Fuhre mit einer Wahrscheinlichkeit von 30% erkennen.
Das Unternehmen teilt nun mit, dass es mehr als 50% Erkennungsrate als Ziel hat. Daher erhöhen wir nun den Wert für n auf 2. Dabei müssen wir aber bedenken, dass die hypergeometrische Verteilung nur ermittelt, mit welcher Wahrscheinlichkeit unter den gezogenen Objekten exakt x Stück Treffer sind. Wir wollen aber wissen, wie hoch die Wahrscheinlichkeit von 1 oder 2 Treffern bei zwei Zügen ist. Daher können wir nun entweder h(1|50, 15, 2) + h(2|50, 15, 2) berechnen, oder alternativ die Wahrscheinlichkeit des Gegenteils (0 Treffer) ermitteln und das Ergebnis von 1 abziehen: 1 - h(0|50, 15, 2). Wir entscheiden uns für den zweiten Weg, da er weniger Arbeit erfordert:
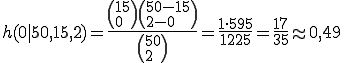 Das ziehen wir nun von 1 ab und erhalten 0,51 als Wahrscheinlichkeit für ein oder zwei Treffer. Das ist knapp mehr als die geforderten 50%. Es reicht also in der Regel aus, zwei mal zu ziehen, um die verunreinigte Fuhre zu erkennen (vorausgesetzt bei verunreinigten Fuhren sind tatsächlich 15 von 50 Päckchen bzw. 30% aller Päckchen verunreinigt).
Das ziehen wir nun von 1 ab und erhalten 0,51 als Wahrscheinlichkeit für ein oder zwei Treffer. Das ist knapp mehr als die geforderten 50%. Es reicht also in der Regel aus, zwei mal zu ziehen, um die verunreinigte Fuhre zu erkennen (vorausgesetzt bei verunreinigten Fuhren sind tatsächlich 15 von 50 Päckchen bzw. 30% aller Päckchen verunreinigt).
Der Erwartungswert errechnet sich für die hypergeometrische Verteilung genauso wie bei der Binomialverteilung, nämlich über
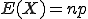 Die Wahrscheinlichkeit (p) kann bestimmt werden indem die Anzahl der Objekte, die Treffer wären durch die Anzahl aller Objekte geteilt wird (
Die Wahrscheinlichkeit (p) kann bestimmt werden indem die Anzahl der Objekte, die Treffer wären durch die Anzahl aller Objekte geteilt wird (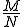 ). Für das vorherige Beispiel (bei zwei mal ziehen) liegt der Erwartungswert demnach bei
). Für das vorherige Beispiel (bei zwei mal ziehen) liegt der Erwartungswert demnach bei
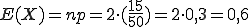 Die Varianz wiederum ergibt sich über
Die Varianz wiederum ergibt sich über
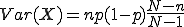 Für das vorherige Beispiel (wieder zwei mal ziehen) lautet der Wert daher
Für das vorherige Beispiel (wieder zwei mal ziehen) lautet der Wert daher
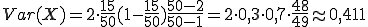
- Hypergeometrische Verteilung: Dient zur Ermittlung der Wahrscheinlichkeit, dass man beim Ziehen von Objekten aus einer Menge von Objekten exakt x Treffer erzielt
Es sind vorhanden: N = Anzahl aller Objekte, M = Anzahl der Objekte, die Treffer wären.
Es werden n Objekte gezogen. - Formel:
- Die hypergeometrische Verteilung geht also vom Ziehen ohne Zurücklegen aus, die Binomialverteilung hingegen vom Ziehen mit Zurücklegen.
- Erwartungswert:
, Varianz:
1. Definition der hypergeometrischen Verteilung
Die hypergeometrische Verteilung ist sozusagen der Bruder der Binomialverteilung. Wir erinnern uns: bei der Binomialverteilung wurde berechnet wie hoch die Wahrscheinlichkeit ist, nach n Wiederholungen eines Experiments (bzw. nach n Zügen) exakt x Treffer erzielt zu haben. Die hypergeometrische Verteilung misst genau das selbe. Der einzige Unterschied ist nur, dass die Binomialverteilung davon ausgeht, dass sich die Wahrscheinlichkeit eines Treffers pro Zug nicht ändert. Sie funktioniert also nach dem Prinzip Ziehen mit Zurücklegen. Die hypergeometrische Verteilung hingegen geht davon aus, dass die Menge aus der gezogen wird begrenzt ist und dass alles was gezogen wurde nicht mehr zurückgelegt wird. Nach jedem Zug (bzw. nach jeder Wiederholung des Experiments) ändert sich also die Wahrscheinlichkeit.
| Binomialverteilung | Hypergeometrische Verteilung | |
| Ziehen | Ziehen mit Zurücklegen | Ziehen ohne Zurücklegen |
| Trefferwahrscheinlichkeit | konstant | ändert sich nach jedem Zug |
| Menge aus der gezogen wird | häufig unbegrenzt (falls nicht unbegrenzt bleibt die Wahrscheinlichkeit aber dennoch konstant, da mit Zurücklegen gezogen wird) |
begrenzt, häufig nur einige wenige Objekte |
Für die Formel müssen nun zuerst folgende Variablen definiert werden:
- N: Die Anzahl aller Objekte, die gezogen werden können (z. B. die Anzahl aller Kugeln in einer Urne)
- M: Die Anzahl der Objekte, die Treffer wären (z. B. nur die roten Kugeln aus einer Urne)
- n: Gibt an, wie oft gezogen werden soll (z. B. fünf Züge)
- x: Anzahl der Treffer auf die getestet werden soll. Ein Wert von x=1 hieße, dass die Wahrscheinlichkeit ermittelt wird, dass man exakt einen Treffer hat.
Die hypergeometrische Verteilung errechnet sich dann über:
2. Beispiel
Angenommen das Unternehmen „Carne Malata International” (kurz: CMI) aus Neapel stellt sie als Statistiker ein. CMI ist ein Lieferant von äußerst preisgünstigem Intensivgeschmackfleisch, das die Darmflora aktiv anregt. Der ehrenwerte CEO beschreibt sein Unternehmen:
Zitat: CEO
Doch das Unternehmen hat Probleme bei seiner Qualitätskontrolle. Immer wieder vermischt sich das Spezialfleisch mit zu qualitativem Fleisch aus anderen Produktionen. Das ist bedenklich, denn die Kunden könnten bei zu hoher Qualität in Anbetracht des Preises glauben, dass sie Hehlerware kaufen und aus Angst vor juristischen Konsequenzen den Anbieter wechseln. Daher erhalten sie nun ihren ersten Auftrag: eine Fuhre mit 50 Päckchen Fleisch soll ausgeliefert werden. Bisher wurde immer zur Kontrolle nur ein Päckchen Fleisch entnommen und geprüft. Das Unternehmen will nun wissen, ob dies ein guter Test ist. Dabei ist bekannt, dass verunreinigte Fuhren gewöhnlich 15 Päckchen schädliches Qualitätsfleisch enthalten.Wir sind ein Lieferant von Fleisch, der sich auf preisbewusste Käufer eingestellt hat. Durch größte Anstrengungen bei der Kostensenkung können wir inzwischen schon für 0,5€ pro kg liefern. Das ist ein Angebot, das kein Käufer ablehnen kann. Manche Personen von selbsternannten „Gesundheitsämtern” belegen unser Produkt aufgrund des Preises mit sehr abfälligen Bezeichnungen. Die Wahrheit ist aber, dass es ein Traum für jeden Kunden ist. Auf der Zunge explodiert es geradezu vor Geschmack — und im Magen aktiviert es die Darmbakterien so sehr, dass man das noch den ganzen Tag spürt!
Aus der Aufgabenstellung gehen folgende Variablen hervor:
- N = 50 (Alle Päckchen in der Fuhre)
- M = 15 (Das Qualitätsfleisch, das man nicht ausliefern will)
- n = 1 (Ein Päckchen wird bisher entnommen und geprüft)
- x = 1 (Da ausgerechnet werden soll wie hoch die Wahrscheinlichkeit ist, dass das eine entnommene Päckchen ein Treffer ist)
Das Unternehmen teilt nun mit, dass es mehr als 50% Erkennungsrate als Ziel hat. Daher erhöhen wir nun den Wert für n auf 2. Dabei müssen wir aber bedenken, dass die hypergeometrische Verteilung nur ermittelt, mit welcher Wahrscheinlichkeit unter den gezogenen Objekten exakt x Stück Treffer sind. Wir wollen aber wissen, wie hoch die Wahrscheinlichkeit von 1 oder 2 Treffern bei zwei Zügen ist. Daher können wir nun entweder h(1|50, 15, 2) + h(2|50, 15, 2) berechnen, oder alternativ die Wahrscheinlichkeit des Gegenteils (0 Treffer) ermitteln und das Ergebnis von 1 abziehen: 1 - h(0|50, 15, 2). Wir entscheiden uns für den zweiten Weg, da er weniger Arbeit erfordert:
3. Erwartungswert und Varianz
Der Erwartungswert errechnet sich für die hypergeometrische Verteilung genauso wie bei der Binomialverteilung, nämlich über