1. Einleitung
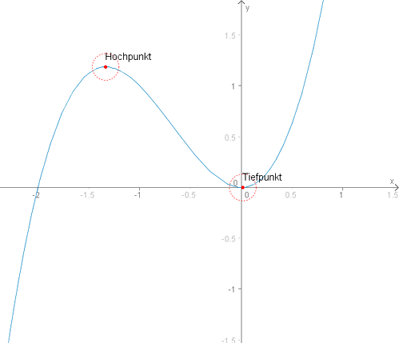
In den meisten Graphen, die man in der Schule bearbeiten muss, gibt es sogenannte "Extremstellen" (auch: Extremwerte, Extrempunkte). Wie der Name bereits andeutet, sind das diejenigen Stellen, an denen der Graph - allgemein ausgedrückt - in irgendeiner Weise besonders ausgeprägt ist. Man unterteilt die Extremstellen in Hochpunkte und Tiefpunkte bzw. Maxima (=Hochpunkte) und Minima (=Tiefpunkte).
Extremstellen sind also sozusagen alle kleinen "Hügel" und "Täler" im Graphen.
Man unterscheidet weiterhin zwischen "lokalen" Maxima/Minima und "absoluten". Die absoluten gelten für die gesamten Graphen (also z.B. der höchste Punkte im gesamten Graphen), während die lokalen nur für kleine Abschnitte gelten (z.B. zwei kleine Hochpunkte nebeneinander). Die lokalen Maxima/Minima können also mehrmals auftreten, die absoluten jeweils nur ein Mal im gesamten Graphen (im obigen Graphen gibt es ein absolutes Minimum und ein absolutes Maximum).
Graphen müssen allerdings weder Hochpunkte noch Tiefpunkte haben. In der Regel haben die Graphen, die man in der Schule bearbeiten muss, diese aber.
2. Finden von Extremstellen
Extremstellen zu finden funktioniert immer nach dem- selben Schema:
- Ableitung bilden (also f'(x) von f(x))
- Ableitung gleich Null setzen und x ausrechnen.
- f'(x)=0 ist notwendige Bedingung, d.h. sie ist erforderlich um Extremstelle zu bestimmen, aber nicht ausreichend um zu beweisen, dass es eine ist.
Beispiel:
Ableitung f'(x) gleich Null setzen und x bestimmen:
Um jetzt das ganze komplett zu machen, müsste man diese x-Werte nun noch in f(x) einsetzen, um die zugehörigen y-Werte zu erhalten (sodass man also einen richtigen Punkt im Koordinatensystem erhält).
Die verwendete Funktion f(x) war übrigens die selbe, die auch oben im Bild zu sehen ist.
Wie man leicht erkennen kann, stimmen die errechneten Extremstellen mit denen im Bild überein.
3. Hochpunkt oder Tiefpunkt?
Hat man diese Koordinaten nun errechnet, dann weiß man schon mal wo die Extremstelle ist. Man weiß aber noch nicht, ob die Extremstelle nun ein Tiefpunkt oder ein Hochpunkt ist.
Will man eine Antwort auf diese Frage (Hochpunkt oder Tiefpunkt?) finden, dann kann man eine von zwei Methoden verwenden:
- Prüfung über Vorzeichenwechsel
- Überprüfung mit der 2.Ableitung
4. Prüfung über Vorzeichenwechsel
Bei der Prüfung über den Vorzeichenwechsel setzt man in die Ableitung f ' (x) zwei x-Werte ein: Einen knapp vor der Extremstelle und einen knapp danach. Die Theorie ist, dass bei einem Hochpunkt die Steigung davor positiv ist (der Graph steigt zum Extrempunkt hoch) und danach negativ ist (er fällt vom Extremwert herab.
Beim Tiefpunkt sollte es entsprechend umgekehrt sein: Die Steigung sollte erst negativ und dann positiv sein (Graph fällt erst und steigt dann nach dem Tiefpunkt wieder).
Man setzt also einfach zwei x-Werte ein und prüft welches Vorzeichen jeweils das Ergebnis hat. Bei der Wahl der x-Werte sollte man natürlich welche nehmen, die möglichst nah an der Extremstelle sind - und zwar näher, als die nächste andere Extremstelle im Graphen (sofern vorhanden).
Beispiel:
Wir untersuchen eine Extremstelle aus dem Graphen, der bereits oben untersucht wurde.
Gewählt wird die Extremstelle an Position x=0.
Wir setzen zuerst -1 und dann +1 ein (bei -4/3 liegt bereits die nächste Extremstelle, man sollte also auf keinen Fall -2 nehmen).
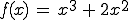
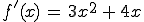
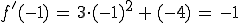
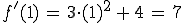
Die Steigung ist also zuerst negativ (-1) und dann positiv (+7) - der Graph fällt also erst und steigt dann wieder. Es liegt also ein Tiefpunkt vor.
Schaut man oben im Bild wird man auch erkennen, dass beim x-Wert 0 in der Tat ein Tiefpunkt ist.
Gewählt wird die Extremstelle an Position x=0.
Wir setzen zuerst -1 und dann +1 ein (bei -4/3 liegt bereits die nächste Extremstelle, man sollte also auf keinen Fall -2 nehmen).
Die Steigung ist also zuerst negativ (-1) und dann positiv (+7) - der Graph fällt also erst und steigt dann wieder. Es liegt also ein Tiefpunkt vor.
Schaut man oben im Bild wird man auch erkennen, dass beim x-Wert 0 in der Tat ein Tiefpunkt ist.
Wichtig: Liegt kein Vorzeichenwechsel vor (von + nach + / von - nach -), dann ist der errechnete Punkt keine Extremstelle, sondern ein Wendepunkt oder Sattelpunkt.
5. Prüfung über 2. Ableitung
Man kann auch alternativ über die 2. Ableitung testen. Man prüft also sozusagen die Steigung der Steigung des Graphen an Position x. Das ist schon reichlich schwer sich das vorzustellen - vor allem wenn man noch nicht oft mit Graphen gearbeitet hat. Man sollte es also am besten einfach akzeptieren ;)
Die 2. Ableitung muss ungleich 0 sein, wenn es sich um einen Extrempunkt handelt. Dies ist die hinreichende Bedingung für Extrempunkte, da sie beweist, dass es kein Sattelpunkt ist. Beide Bedingungen zusammen beweisen, dass es ein Extrempunkt ist.
Bei diesem Prüfverfahren muss man nur einen Test machen und zwar setzt man den x-Wert der Extremstelle in die zweite Ableitung ein und rechnet das Ganze aus. Man schaut dann, welcher von insgesamt 3 möglichen Fällen auftritt:
- Das Vorzeichen des Ergebnisses ist negativ (Ergebnis<0): Extremstelle ist ein Hochpunkt.
- Das Ergebnis ist gleich Null (Ergebnis=0): Der Punkt ist keine Extremstelle, sondern ein Wendepunkt/Sattelpunkt.
- Das Vorzeichen des Ergebnisses ist positiv (Ergebnis>0): Extremstelle ist ein Tiefpunkt
Beispiel:
Es wird wieder die bereits bekannte Funktion verwendet. Diesmal wird aber auch noch eine zweite Ableitung benötigt, in die man dann den x-Wert der Extremstelle einsetzt.
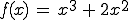
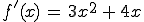
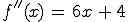
Untersucht wird wieder die Extremstelle am x-Wert 0.
Diesmal indem man den x-Wert 0 in die zweite Ableitung einsetzt, ausrechnet und das Ergebnis prüft.
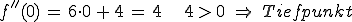
Das Ergebnis ist also wieder das gleiche wie auch bei der Prüfung über Vorzeichenwechsel.
Untersucht wird wieder die Extremstelle am x-Wert 0.
Diesmal indem man den x-Wert 0 in die zweite Ableitung einsetzt, ausrechnet und das Ergebnis prüft.
Das Ergebnis ist also wieder das gleiche wie auch bei der Prüfung über Vorzeichenwechsel.