1. Einleitung
Sehr häufig wird man in der Vektorrechnung zwischen den einzelnen Ebenengleichungen umrechnen müssen - sei es, weil das in der Aufgabe gefordert wird, oder weil eine andere Form der Ebene eine bestimmte Rechnung vereinfacht.
Es gibt 3 Ebenengleichungen: Parameterform, Normalenform, Koordinatenform. Das Umrechnen zwischen den einzelnen Formen ist verschieden schwierig. So ist es mit Abstand am einfachsten von der Normalenform zur Koordinatenform umzurechnen. Von der Parameterform zur Normalenform/Koordinatenform ist es allerdings recht langwierig, da man hier erst einen Normalenvektor bilden muss.
Es gibt vier wesentliche Umformungen zwischen den Ebenengleichungen (von sechs möglichen):
- 1. Von Parameterform zur Normalenform
- 2. Von Normalenform zur Koordinatenform
- 3. Von Koordinatenform zur Normalenform
- 4. Von Koordinatenform zur Parameterform
Die Umrechnungen "von Normalenform zur Parameterform" und "von Parameterform zur Koordinatenform" kann man sich sparen, da diese bereits durch die anderen Umrechnungen abgedeckt werden (und da das Umrechnen zwischen Koordinatenform und Normalenform ohnehin kinderleicht ist).
2. 1. Von Parameterform zur Normalenform
Bei dieser Umwandlung muss man einen Normalenvektor der Ebene finden, da dieser für eine Ebene in Normalenform notwendig ist. Den Punkt in der Ebene kann man aber weiterverwenden.
Der Normalenvektor liegt immer orthogonal (also im rechten Winkel) zur Ebene. Da beide Richtungsvektoren, die in der Parameterform gegeben sind, auch in der Ebene liegen, reicht es, einen orthogonalen Vektor zu diesen beiden Richtungsvektoren zu bilden. Einen Vektor, der orthogonal zu zwei anderen Vektoren ist, findet man, indem man das Vektorprodukt der beiden Vektoren bildet.
Will man also von der Parameterform zur Normalenform umrechnen, dann muss man nur das Vektorprodukt der beiden Richtungsvektoren bilden. Den Stützvektor kann man weiterverwenden.
Beispiel:
Gegeben:
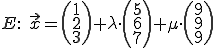
Vektorprodukt der beiden Richtungsvektoren bilden:
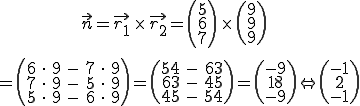
Das Ergebnis ist der Normalenvektor der Ebene
(im letzten Schritt gekürzt, da für den Normalenvektor nur die Richtung wichtig ist, nicht aber die Länge).
Jetzt können der Stützvektor von der Parameterform und der Normalenvektor in die Normalenform übertragen werden:
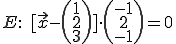
Vektorprodukt der beiden Richtungsvektoren bilden:
Das Ergebnis ist der Normalenvektor der Ebene
(im letzten Schritt gekürzt, da für den Normalenvektor nur die Richtung wichtig ist, nicht aber die Länge).
Jetzt können der Stützvektor von der Parameterform und der Normalenvektor in die Normalenform übertragen werden:
3. 2. Von Normalenform zur Koordinatenform
Die wohl leichteste Umrechnung zwischen Ebenen. Hier muss man nichts anderes tun als einfach auszumultiplizieren (mit Hilfe vom Skalarprodukt).
Beispiel:
Gegeben:
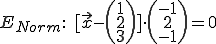
Jetzt wird einfach ausmultipliziert:
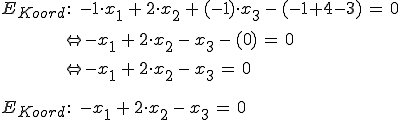
Gewöhnlich bekommt man bei dem, was hier im 1. Schritt in der Klammer steht (-1+4-3), einen Wert ungleich 0 heraus. Der muss dann auf die rechte Seite vom Gleichzeichen gebracht werden.
Jetzt wird einfach ausmultipliziert:
Gewöhnlich bekommt man bei dem, was hier im 1. Schritt in der Klammer steht (-1+4-3), einen Wert ungleich 0 heraus. Der muss dann auf die rechte Seite vom Gleichzeichen gebracht werden.
4. 3. Von Koordinatenform zur Normalenform
Um von der Koordinatenform zur Normalenform zu kommen, muss man nur einen einzigen Punkt in der Ebene bestimmen. Den Normalenvektor, der für die Normalenform notwendig ist, kann man einfach aus der Koordinatenform ablesen.
Beispiel:
Gegeben:
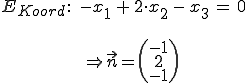
Nun muss man einen Punkt in der Ebene finden.
Das geht am einfachsten, indem man Werte für x1, x2 und x3 so einsetzt, dass ein wahres Ergebnis herauskommt (also 0=0).
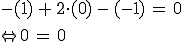
Der Punkt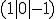
liegt also in der Ebene.
Punkt und Normalenvektor können jetzt einfach für eine Ebene in Normalenform verwendet werden:
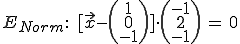
Nun muss man einen Punkt in der Ebene finden.
Das geht am einfachsten, indem man Werte für x1, x2 und x3 so einsetzt, dass ein wahres Ergebnis herauskommt (also 0=0).
Der Punkt
Punkt und Normalenvektor können jetzt einfach für eine Ebene in Normalenform verwendet werden:
5. 4. Von Koordinatenform zur Parameterform
Der einfachste Weg, um von der Koordinaten- zur Parameterform zu kommen ist es, sich einfach über die Koordinatenform drei Punkte in der Ebene zu suchen. Dazu muss man lediglich beliebige Punkte einsetzen und prüfen, ob das Ergebnis wahr ist (dann liegt der Punkt in der Ebene).
Hat man die drei Punkte, dann daraus einfach eine Ebene in Parameterform bilden: Ortsvektor zu einem der drei Punkte als Stützvektor und zwei linear unabhängige Vektoren bilden, die dann als Richtungsvektoren verwendet werden.
Beispiel:
Gegeben:
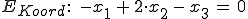
Drei Punkte in der Ebene suchen
(einfach einsetzen und prüfen, ob das Ergebnis wahr ist):
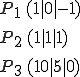
Daraus kann man nun eine Ebene in Parameterform bilden:
Stützvektor: Ortsvektor P1, Richtungsvektor 1: P1P2, Richtungsvektor 2: P1P3
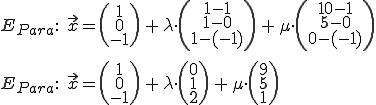
Drei Punkte in der Ebene suchen
(einfach einsetzen und prüfen, ob das Ergebnis wahr ist):
Daraus kann man nun eine Ebene in Parameterform bilden:
Stützvektor: Ortsvektor P1, Richtungsvektor 1: P1P2, Richtungsvektor 2: P1P3
6. Links
Abschließend noch ein paar Videos, die die jeweiligen Rechnungen verdeutlichen sollten:
Kommentare (58)
Von neu nach altWir bitten um ihr Verständnis.
gibt es die o.a. hilfreichen Infos auch als pdf? AndreaS
(einfach einsetzen und prüfen, ob das Ergebnis wahr ist):"
Selten so etwas Dämliches gelesen
Danke für das Erstellen.
Echt hilfreich - so kann man einfach die Überformungen nochmal anschaun
Und die restlichen 2 kann man ja notfalls über einen Umweg bekommen.
1. Zeile fängt man links oben an.
2. Zeilen: links unten (oder man macht den VZW)
3. Zeilen: links oben
sagt mal: Wir haben gelernt, dass die mittlere Zeile des Vektorproduktes ein Vorzeichenwechsel bekommt. Jetzt lasst ihr die zwei aber zwei sein und fuegt ihr kein Minus an. *Gruebel* was ist denn nu richtig??